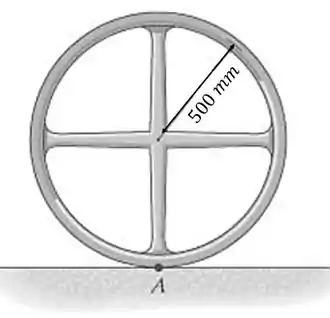
A roda consiste num anel fino de e quatro raios feitos de barras delgadas, cada uma com com . Determine o momento de inércia da roda em relação a um eixo que é perpendicular à página e passa pelo ponto . Suponha que as barras e o anel são homogêneos.
Passo 1
Para resolver este problema vamos ter que aplicar o teorema dos eixos paralelos. Repare que temos duas barras e um anel, então vamos calcular o momento de inércia deles com relação ao eixo que passa pelo centro de gravidade .
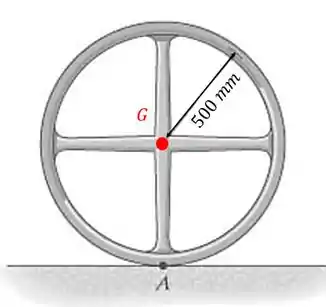
O momento de inércia com relação a um eixo que passa pelo centro de gravidade é:
Mas sabemos que:
E repare que no enunciado foram dadas as massas de cada elemento que compõe o corpo. Como o raio é constante, podemos dizer que o momento de inércia com relação ao eixo que passa pelo centro de gravidade é:
O momento de inércia de um anel fino é tabelado:
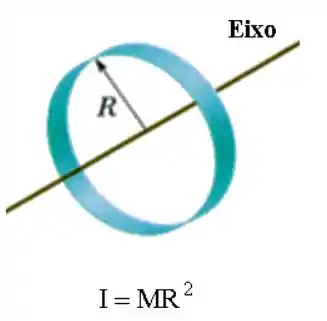
Onde, é o raio do anel. Então, no nosso caso teremos:
Temos que a massa do anel é e a distância do anel até o eixo é igual ao valor do raio de :
Passo 2
Para as barras vamos fazer a mesma coisa. Sabemos que o momento de inércia de uma barra delgada também é tabelado e vale:
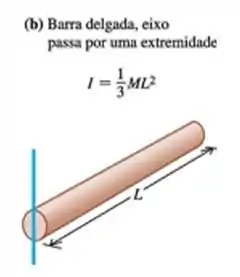
Como estamos considerando o quatro barras, o comprimento de cada barra será de igual ao valor do raio do anel:
Então:
A massa da barra vale :
Então, o momento de inércia com relação ao eixo que passa pelo centro de gravidade da peça é igual a soma do momento de inércia com relação ao mesmo eixo de cada parte que compõe a figura:
Não esqueça que temos quatro barras e só calculamos o momento de inércia para uma delas:
Passo 3
Nosso próximo passo é calcular o momento de inércia em relação ao eixo perpendicular à figura e que passa pelo ponto . Para isso, temos que saber a distância entre os eixos paralelos:
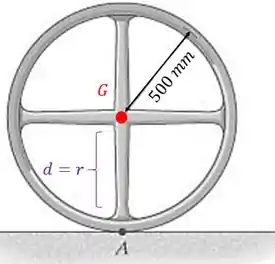
Então, vamos usar o teorema dos eixos paralelos:
Lembrando que a massa do anel é e a massa da barra é de :