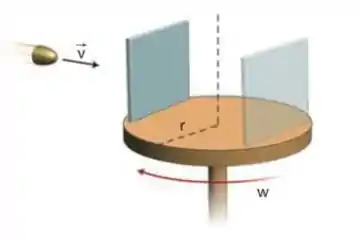
Um disco de raio gira com velocidade angular constante. Na borda do disco, está presa uma placa fina de material facilmente perfurável. Um projétil é disparado com velocidade em direção ao eixo do disco, conforme mostra a figura, e fura a placa no ponto . Enquanto o projétil prossegue sua trajetória sobre o disco, a placa gira meia circunferência, de forma que o projétil atravessa mais uma vez o mesmo orifício que havia perfurado. Considere a velocidade do projétil constante e sua trajetória retilínea.

O módulo da velocidade do projétil é:

A)

B)

C)

D)

E)

Vamos lá!

Primeira coisa: qual é a distancia que a bala andou? , certo? Pois ela anda por cima do disco, e passa pelo ponto A nas extremidades do disco.

Segunda coisa: qual o tempo que a bala leva pra percorrer esse comprimento?

Bom, foi o tempo do disco fazer meia volta. Como a gente descobre esse tempo?

Lembra que o tempo necessário para completar uma volta, em trajetórias circulares, é chamado de período ?

Então, se o disco completa meia volta, quer dizer que temos metade do período , .

Podemos relacionar o período com a aceleração angular:

Então:

E esse foi o tempo que a bala demorou pra percorrer a distancia de . Agora já temos a distancia e o tempo, então é só calcular a velocidade:

Show?!!