Para qual dos seguintes movimentos de um objeto a aceleração deve ser sempre zero:

. Qualquer movimento em linha reta

. Qualquer movimento em uma circunferência

. Movimento harmônico simples (como o de um pêndulo)

Marque a alternativa correta:

A. Somente

B. Somente

C. e

D. e

E. Nenhum dos movimentos

Queremos saber em qual deles necessariamente não temos aceleração.

Para responder isso, acho que fica mais fácil visualizando cada movimento. Vamos começar com:

. Qualquer movimento em linha reta

Bom, se podemos ter qualquer movimento em linha reta, podemos muito bem ter um movimento retilíneo acelerado, como por exemplo, um carro freando:

. Qualquer movimento em uma circunferência

Apenas pela natureza de um movimento circular, necessariamente temos uma aceleração chamada aceleração centrípeta.

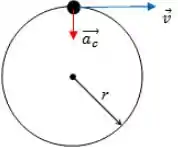
Mas por que necessariamente deve existir uma aceleração centrípeta?

A ideia é bem simples...

Uma aceleração nada mais é do que uma variação na velocidade.

Portanto, para que um corpo realize uma trajetória circular, seu vetor velocidade deve mudar de direção. Essa variação na direção do vetor velocidade é causada por uma aceleração que aponta para o centro da trajetória (aceleração centrípeta).

. Movimento harmônico simples (como o de um pêndulo)

Um movimento harmônico simples nada mais é do que um movimento que se repete ao longo de um intervalo de tempo, ou seja, um movimento periódico.

Podemos ter um pêndulo:

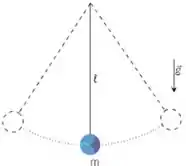
Ele balança de um lado para o outro, sempre num mesmo intervalo de tempo (período).

Ou um sistema massa-mola:

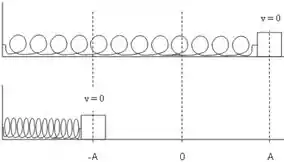
O bloquinho vai e volta, conforme a mola comprime e estica num mesmo intervalo de tempo (período).

Bom, para esses caras a ideia é a mesma...

Se há mudança de velocidade, há aceleração.

Portanto, vimos que em nenhuma das opções , e o movimento deve ser sempre sem aceleração.

Ficamos com a letra E.