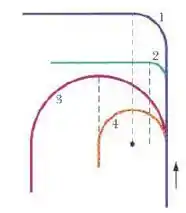
A figura abaixo mostra quatro trilhos [semicírculos ou quartos de círculo) que podem ser usados por um trem que se move com velocidade escalar constante. Ordene os trilhos de acordo com o módulo da aceleração do trem no trecho curvo, em ordem descrescente.
Passo 1
Ah, temos aqui 4 movimentos circulares. Podemos notar que os raios das trajetórias são diferentes entre si. O enunciado disse pra gente que a velocidade é constante, e como é o mesmo trem para cada curva será a mesma velocidade independente do raio da curva.
Sabendo disso a gente pode usar a equação da aceleração centrípeta e como a velocidade é constante só dependeremos do raio da trajetória pra ordenar as acelerações.
Como o raio está no denominador, quanto maior for o raio menor será a aceleração, beleza?
Passo 2
Vamos olhar a figura e ordenar o tamanho dos raios.
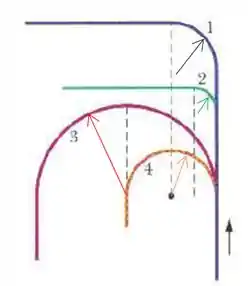
O menor raio aqui é o raio da curva , e se liga a geometria dela pouco importa, o que importa é o tamanho do raio, beleza?
Os raios das curvas e são iguais e maiores que o da curva 2, e como eu disse antes não importa a geometria dessas curvas e só o tamanho dos raios.
O raio da curva 3 é o maior de todos.
Sendo assim ordenamos os raios.
E a gente viu antes que o menor raio nos dará a maior aceleração centrípeta, então é só inverter essa ordem ai pras acelerações: