Uma partícula em trajetória circular de raio tem um vetor aceleração que em um certo instante faz um ângulo com o vetor velocidade . Podemos afirmar que nesse instante
- O módulo da velocidade da partícula é igual a ;
- O módulo da velocidade da partícula é igual a ;
- A aceleração da partícula tem módulo ;
- O módulo da velocidade da partícula está aumentando;
- O módulo da velocidade da partícula está diminuindo;
Passo 1
No movimento circular, a velocidade é tangencial ao movimento.
Como a aceleração possui um ângulo de com a velocidade, significa que ela não é somente a aceleração centrípeta mas também tem a componente tangencial.
A aceleração tangencial é no mesmo sentido da velocidade isso porque o ângulo entre a velocidade e a aceleração é menor que .Vamos fazer um desenho para visualizar melhor.
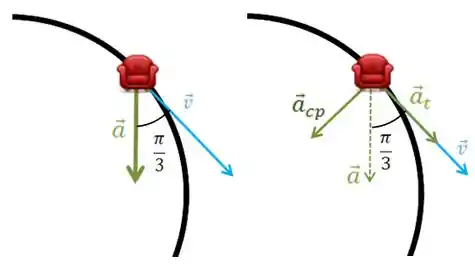
Repara no desenho, que a aceleração tangencial é no mesmo sentido que a velocidade então o módulo da velocidade está aumentando. Isso tá dito na opção (d)!
Passo 2
Vamos justificar por que as outras estão erradas?
A letra (e) tá errada por que ela fala o contrário da letra (d)!
Passo 3
As letras (a) e (b) dizem um certo valor pra velocidade! Como a trajetória é circular vamos ter que a velocidade se relaciona com a aceleração centrípeta
E a aceleração centrípeta é uma componente da aceleração, que, pela figura acima, é dada por
Assim
O que não tem nada a ver com as opções né? rsrsrs Nem na unidade tá batendo!
Passo 4
A aceleração da partícula tem duas componentes e podemos escrever o seguinte
Assim o módulo da aceleração será
Como
O módulo da aceleração da partícula será
Que seria se a aceleração tangencial fosse nula! Como não é, então o item (c) tá errado também!
Resposta
Letra D