Em um treinamento, um veículo é colocado em uma pista circular e percorre a cada . Sabendo que o diâmetro da pista é , podemos afirmar que o módulo da aceleração centrípeta do veículo, em , é igual a:
(a)
(b)
(c)
(d)
(e)
Passo 1
Ele fala diretamente o que ele quer: A aceleração centrípeta, que é aquela que aponta sempre pro centro da trajetória, e vale:
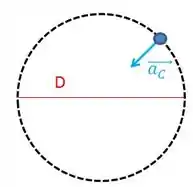
Mas aí a gente vai ler o enunciado e não sabemos nem a velocidade e nem o raio...eita!

Acompanha aqui comigo que é sucesso garantido.
Passo 2
Ele não falou a velocidade, né? Mas ele disse a distância que o carrinho percorreu e quanto tempo ele demorou pra percorrer. Aí fica moleza:
Então:
Maravilha!
E o raio?
Bem ele falou o diâmetro, e sabemos que:
Show! Agora é substituir na fórmula da aceleração centrípeta.
Passo 3
Resolvendo isso daí:
Prontinho! Vamos pra próxima!
Resposta
Alternativa C.