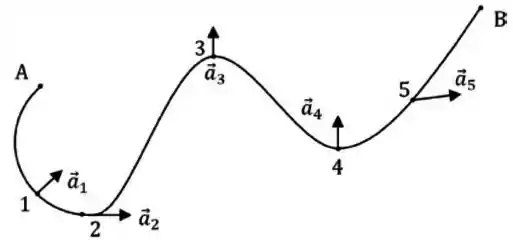
A figura mostra a trajetória no plano horizontal de uma partícula que se desloca da posição A para a posição final B. Dentre as setas marcadas nos pontos 1 a 5 da figura, as que podem representar o vetor aceleração da partícula no ponto considerado são
(a) e
(b) e
(c) e
(d) e
(e) e
Passo 1
Com a exceção do ponto 5, todos os pontos indicados na figura são pontos de curva, onde a trajetória da partícula pode ser comparada a um movimento circular.
Nesses pontos de curva, temos sempre 2 tipos de aceleração: a aceleração centrípeta, que aponta pro centro da curva e a aceleração tangencial, que é tangente à trajetória.
Passo 2
O detalhe crucial é que a partícula sempre tem aceleração centrípeta quando faz uma curva. A partícula, quando faz a curva, está mudando de direção. E é justamente a aceleração centrípeta que faz essa mudança de direção.
Por outro lado, a partícula nem sempre tem aceleração tangencial. Essa é associada com a variação do valor da velocidade da partícula. Então se a partícula estiver lá de boas, mantendo sua velocidade constante, não vai ter aceleração tangencial.
Passo 3
Conclusão disso tudo: numa questão dessas, temos que sempre considerar a aceleração centrípeta; numa curva a aceleração nunca é só tangencial. Ou seja, o vetor aceleração da partícula tem que sempre apontar pelo menos um pouco pra dentro da curva.
Passo 4
Agora vamos ver os vetores aceleração um por um!
- O vetor aponta pra dentro da curva, então tudo certo com ele!
- O vetor é só tangencial, então ele não pode representar a aceleração da partícula nesse ponto.
- O vetor está apontando pra fora da curva, então podemos eliminar.
- Nada de errado com o vetor , ele está apontando pra dentro da curva.
- O vetor é um caso à parte. A partícula não está mais fazendo uma curva, e sim um movimento retilíneo, então o vetor aceleração dela tem que apontar na direção dessa reta. Mas não é o caso, o aponta pra fora da reta, então está errado!
Então os vetores corretos são o e o !
Resposta
Alternativa (a)