UFSCAR, Sem Campus, Física 1, AV1 - 2021.1 - Prof° Raphael Santarelli, Questão 4b
Uma partícula se move em uma trajetória circular horizontal no plano , com velocidade escalar constante. No instante , a partícula possui velocidade e aceleração no sentido positivo de . No instante , a partícula possui velocidade e aceleração no sentido positivo de . Considere a diferença é menor que um período de rotação.
Qual o período de rotação (tempo para dar uma volta completa)?
Passo 1
Oiie, tudo certinho?
Temos aqui uma partícula se movendo em uma trajetória circular sobre o plano , o enunciado nos dá algumas informações sobre instantes da trajetória, como por exemplo, nos indica que no instante , a velocidade da partícula é tal que
da mesma forma, temos que em , a velocidade é tal que
O enunciado também nos dá informações sobre a direção da aceleração nestes dois instantes, no primeiro instante a aceleração está no sentido positivo de , e no segundo instante, está no sentido positivo de . Por último, nos é afirmado que , em que é um período de rotação! Belezinha?
Para esta alternativa vamos precisar obter o período de rotação! Podemos usar a informação sobre o posicionamento dos vetores velocidade nos instantes de tempo dados, assim como no esquema que obtemos na alternativa anterior
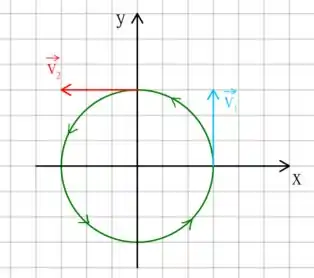
Com isso em mãos podemos lembrar o que período significa, e teremos diretamente a nossa resposta! Saca só!
Passo 2
Temos que ao longo do movimento a velocidade da partícula se mantém constante
lembrando que o período é o tempo que leva para a partícula completar a circunferência do círculo, e tendo em vista o esquema que montamos na alternativa anterior, você pode notar que o intervalo de tempo equivale a um quarto da circunferência! Ou seja, temos que o período completo será
Ou, simplesmente
Maravilha! Mais uma alternativa já foi! Te vejo na próxima! Inté!