Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Isolamento de Raízes e Método Gráfico

Ver Teoria
Exercício 41235678910

Enunciado

Ache o valor de x   para que f ( x ) seja mínimo:

f x = cosh ⁡ x 2 - 2 x

Passo 1

Que isso, cara?

Valor mínimo? Não vimos nada disso até agora!

Relaxaaa Aí!

Vamos só relembrando de quando foi se estudou Cálculo de derivadas. O valor máximo ou mínimo de uma função é dada quando a sua derivada é zero.

Então é isso o que temos que fazer:

f ' x = 2 x ∙ s e n h x 2 - 2 = 0

Passo 2

Agora deu uma clareada? Temos uma expressão bem mais parecida com os casos mais comuns.

2 x ∙ s e n h x 2 = 2

Cortando os 2:

x ∙ s e n h x 2 = 1

Ou melhor:

s e n h x 2 = 1 x

h x = s e n h x 2     e   g x = 1 x

Passo 3

Mas pera aí, né? Você não é obrigado a saber a função de s e n h ( x 2 ) . Se rolar de na prova cair alguma questão que você não sabe o gráfico, pega a calculadora (digitando as teclas hyp e sin) e vai jogando alguns valores pra f 0 , f 1 ,   f 2 ,   f 3 ,   f ( 4 ) e vai ligando os pontos, até ele ter uma boa cara de gráfico mesmo.

Fazendo isso aqui:

f 0 = 0

f 1 = 1,17

f 2 = 27,28

f 3 = 4051,54

É, um gráfico que cresce super rápido. Fazendo mais alguns valores você vai chegar num negócio assim:

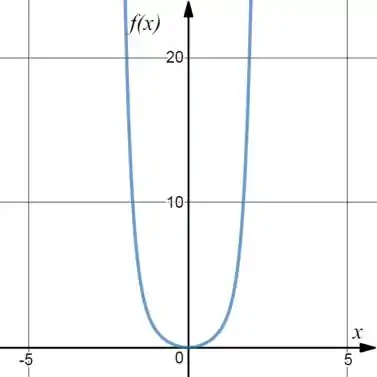
Já pra função g x = 1 x , vai ser:

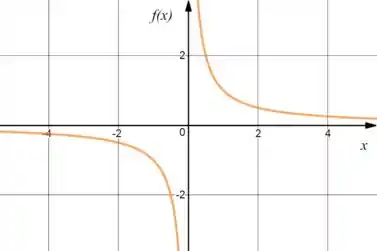
Passo 4

Fazendo a intersecção entre os gráficos, teremos:

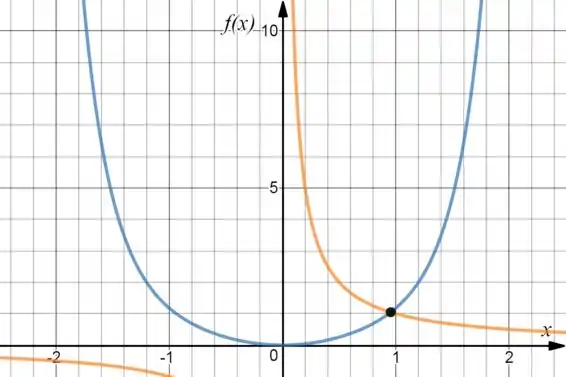
Fazendo uma estimativa pelo gráfico, vamos ter que a raiz dessa função vai ser algo entre 0.9 e 1 .

Logo:

ξ ≅ 0,95

Resposta

ξ ≅ 0,95

Exercícios de Livros Relacionados

Localize graficamente as raízes das equações a seguir: 4c o s ( x )-e 2 x=0 x 2 - t g ( x ) = 0 1 - x l n ( x ) = 0 2 x - 3 x = 0 x 3 + x - 1000 = 0
Seja f ( x ) = x + l n ( x ) que possui um zero no intervalo I = [ 0.2,2 ] . Se o objetivo for obter uma aproximação x k para esta raiz de tal forma que | x k - ϵ |1 0 - 5 , é aconselhável usar o méto
Seja f ( x ) = s e n ( x ) - k x . Encontre os valores positivos de k para que f tenha apenas uma raiz estritamente positiva.Encontre os valores positivos de k para que f tenha três raízes estritament
Considere as seguintes funções:a) 𝜓 1 𝑥 =   2 𝑥 − 1   b) 𝜓 2 𝑥 =   𝑥 2 − 2 𝑥   + 2     c) 𝑥 2 − 3 𝑥 + 3 Verifique que 1 é raiz de todas estas funções. Qual delas você escolheria para obter a
Deseja-se obter a raiz positiva da equação: 𝑏 𝑥 2 + 𝑥 − 𝑎 = 0 ,   𝑎0 ,   𝑏0 ,     através do processo iterativo definido por: 𝑥 𝑘 + 1 = 𝑎 − 𝑏 𝑥 𝑘 2 . Qual a condição que devemos impor para