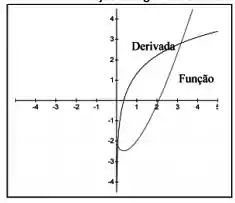
Dada a função , analise esta função e sua derivada pelo gráfico abaixo. Fundamentado neste estudo, responda:
a) Pode existir mais de uma raiz real para a equação ? Justifique.
b) Podemos afirmar que no intervalo existe somente uma raiz real, vemos isso bem analisando o gráfico. Qual teoria discutida anteriormente sustenta esta afirmação quando não temos um gráfico para analisar?
Passo 1
Eita! Questãozinha diferente. Vamos desmembrando-a aos poucos!
1°, na letra a ele nos deu uma função: e ele quer saber se pode existir mais de uma raiz pra essa função aí.
Se liga que sempre quando ele falar em número de raízes você tem que logo associar ao sinal da derivada.
Quando ele pergunta “pode existir mais de uma raiz” pra essa função? Você tem que averiguar, a derivada troca de sinal alguma vez? Se sim, a função pode ter mais de uma raiz.
Nesse caso, no entanto, podemos ver que depois do ponto onde temos o zero da função a derivada é estritamente crescente! Logo, não haverá outra raiz!
Passo 2
Lá na teoria, a gente viu pelo Teorema de Bolzano duas afirmações pra definir e isolar raízes.
- A primeira era que , logo, existem raízes no intervalo .
- Se a função for sempre crescente ou sempre decrescente, só terá no máximo uma raiz.
Nesse caso, a segunda parte do Teorema de Bolzano é a que sustenta a afirmação do texto.

Resposta
Ei, a resposta está no passo a passo :)