Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Isolamento de Raízes e Método Gráfico

Ver Teoria
Exercício 31245678910

Enunciado

Determine um intervalo, de amplitude no máximo igual a 2 , que contenha três raízes da função abaixo:

f x = e x - c o s π x - 1

Passo 1

Vamos lá?

Temos a função f x = e x - cos ⁡ π x - 1 e ele nos pede três raízes num intervalo de duas unidades.

Ideia de como fazer?

Passo 2

É. Eu tenho a sugestão de sempre. Vamos tentar achar os valores da função para x = 0 ,   x = 1   e   x = - 1 .

Bora lá?

f 0 = e 0 - cos ⁡ 0 - 1 = 1 - 1 - 1 = - 1

f 1 = e 1 - cos ⁡ π - 1 = 2,718 - - 1 - 1 = 2,718

f - 1 = e - 1 - cos ⁡ - π - 1 = 1 e + 1 - 1 = 1 e ≅ 0,36

Até agora temos isso aqui:

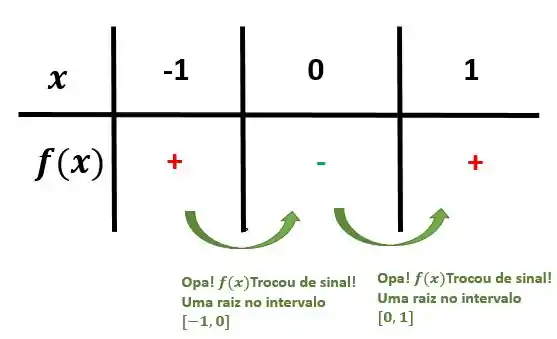
Passo 3

Show! Temos um intervalo de duas unidades, mas só temos duas raízes aí. Vamos tentar ampliar para os valores mais próximos, tipo x = 2   e   x = - 2 pra ver no que rola.

f 2 = e 2 - cos ⁡ 2 π - 1 = 5,39

f - 2 = e - 2 - cos ⁡ - 2 π - 1 = - 1,86

E a tabela de valores ficará mais ou menos assim:

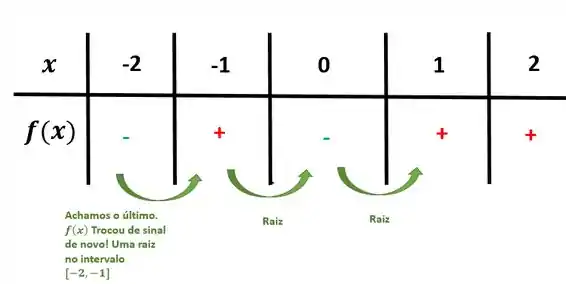
Boa! Isolamos as três raízes. Então acabou o problema, certo?

Errado!

Ele quer um intervalo de no máximo duas unidades. E até agora teríamos o intervalo [ - 2,1 ] que possui 3 unidades.

Passo 4

Já sabendo mais ou menos onde estão as raízes, basta agora chutar um intervalo de até duas unidades, pra ver se ele continua obedecendo os critérios da Lei de Bolzano.

Pra fazer isso, tenho que achar um número x maior que - 2 e menor que - 1   que ainda tenha f ( x ) negativo e também temos que achar um número menor que 1 e maior que 0 que já tenha valor de f ( x ) positivo.

Que números você chutaria?

É, eu também!

x = - 1,5   e   x = 0,5

f - 1,5 = e - 1,5 - cos ⁡ - 1,5 π - 1 = - 0 , 77 69

f 0,5 = e 0,5 - cos ⁡ 0,5 π - 1 = 0,65

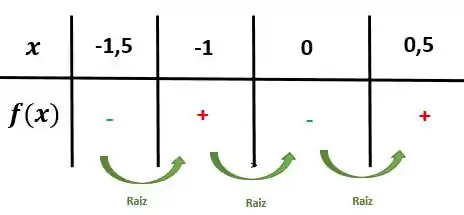
Resolvida a nossa questão. O intervalo é [ - 1,5 ; 0,5 ]

Resposta

[ - 1,5 ; 0,5 ]

Exercícios de Livros Relacionados

Localize graficamente as raízes das equações a seguir: 4c o s ( x )-e 2 x=0 x 2 - t g ( x ) = 0 1 - x l n ( x ) = 0 2 x - 3 x = 0 x 3 + x - 1000 = 0
Seja f ( x ) = x + l n ( x ) que possui um zero no intervalo I = [ 0.2,2 ] . Se o objetivo for obter uma aproximação x k para esta raiz de tal forma que | x k - ϵ |1 0 - 5 , é aconselhável usar o méto
Seja f ( x ) = s e n ( x ) - k x . Encontre os valores positivos de k para que f tenha apenas uma raiz estritamente positiva.Encontre os valores positivos de k para que f tenha três raízes estritament
Considere as seguintes funções:a) 𝜓 1 𝑥 =   2 𝑥 − 1   b) 𝜓 2 𝑥 =   𝑥 2 − 2 𝑥   + 2     c) 𝑥 2 − 3 𝑥 + 3 Verifique que 1 é raiz de todas estas funções. Qual delas você escolheria para obter a
Deseja-se obter a raiz positiva da equação: 𝑏 𝑥 2 + 𝑥 − 𝑎 = 0 ,   𝑎0 ,   𝑏0 ,     através do processo iterativo definido por: 𝑥 𝑘 + 1 = 𝑎 − 𝑏 𝑥 𝑘 2 . Qual a condição que devemos impor para