Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Isolamento de Raízes e Método Gráfico

Ver Teoria
Exercício 51234678910

Enunciado

Localize graficamente as raízes da função a seguir:

a   f x = 2 x - 3 x

a   f x = x 3 + x - 100

Passo 1

Opa, temos duas funçõezinhas aí. Já sabemos o passo a passo, né? Então vamos lá sem mimimi!

:D

Passo 2

a Igualar f x = 0

2 x - 3 x = 0

2 x = 3 x

Tá, temos a nossa h x = g x .

Passo 3

Desenhando o gráfico de cada função, teremos:

h x = 2 x :

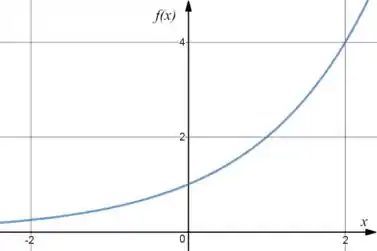
E g ( x ) :

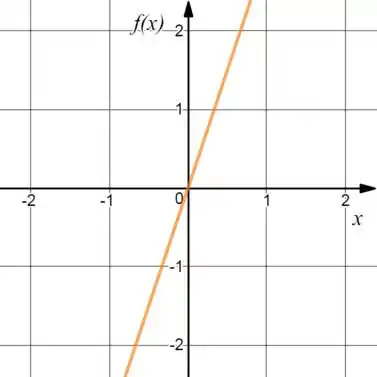
Passo 4

Igualando os dois gráficos, e catando a nossa raiz, vai ficar:

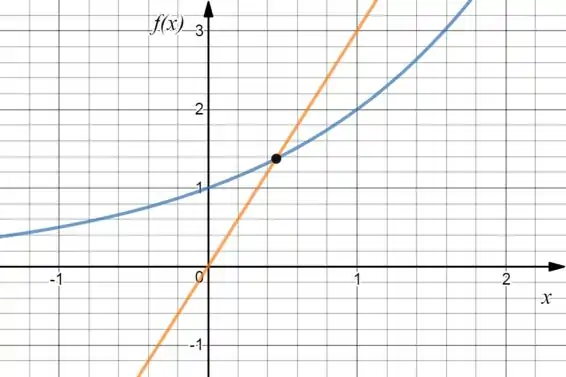
É! Pelo gráfico ele está entre 0.4 e 0,5 , né?

Como a ideia é fazer uma aproximação, podemos dizer que:

ξ a ≅ 0,4 5

Passo 5

b Igualando f x = 0 , teremos:

x 3 + x - 100 = 0

Tá! Agora temos que separar em duas funções h x = g ( x ) em que eu saiba desenhar os gráficos das duas, certo?

Temos algo do 3° grau e algo do 1° grau, então vamos separa-los.

x 3 = - x + 100

h x = x 3

g x = - x + 100

Passo 6

Lembra do gráfico do h x = x ³ ?

É mais ou menos esse aqui:

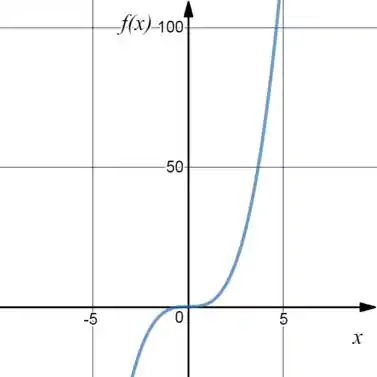
E o g x = - x + 100 é uma reta decrescente, porém “arrastada” em 100 unidades pra cima:

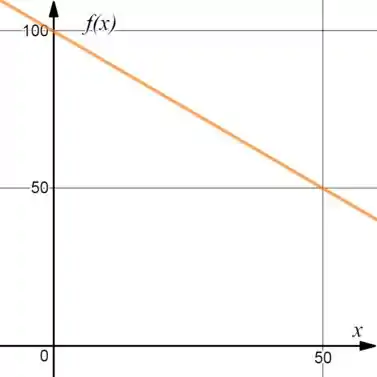
Passo 7

Fazendo a intersecção, ia ficar:

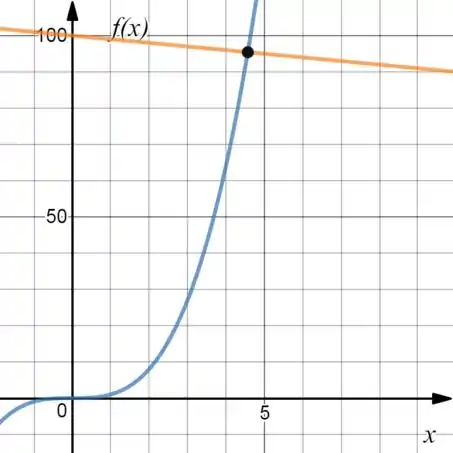
É! Essa raiz está bem no meio do 4 e do 5 . Como queremos a aproximação, vamos dizer que é ξ b ≅ 4,5 .

Só toma cuidado que fazer esse exercício no papel pode gerar bastante imprecisão devido à distância adotada. Cuidado quando for fazer! Usando papel milimetrado e usa boa escala pode te ajudar!

#FicaADica

Resposta

ξ a ≅ 0,4 5

ξ b ≅ 4,5

Exercícios de Livros Relacionados

Localize graficamente as raízes das equações a seguir: 4c o s ( x )-e 2 x=0 x 2 - t g ( x ) = 0 1 - x l n ( x ) = 0 2 x - 3 x = 0 x 3 + x - 1000 = 0
Seja f ( x ) = x + l n ( x ) que possui um zero no intervalo I = [ 0.2,2 ] . Se o objetivo for obter uma aproximação x k para esta raiz de tal forma que | x k - ϵ |1 0 - 5 , é aconselhável usar o méto
Seja f ( x ) = s e n ( x ) - k x . Encontre os valores positivos de k para que f tenha apenas uma raiz estritamente positiva.Encontre os valores positivos de k para que f tenha três raízes estritament
Considere as seguintes funções:a) 𝜓 1 𝑥 =   2 𝑥 − 1   b) 𝜓 2 𝑥 =   𝑥 2 − 2 𝑥   + 2     c) 𝑥 2 − 3 𝑥 + 3 Verifique que 1 é raiz de todas estas funções. Qual delas você escolheria para obter a
Deseja-se obter a raiz positiva da equação: 𝑏 𝑥 2 + 𝑥 − 𝑎 = 0 ,   𝑎0 ,   𝑏0 ,     através do processo iterativo definido por: 𝑥 𝑘 + 1 = 𝑎 − 𝑏 𝑥 𝑘 2 . Qual a condição que devemos impor para