Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Isolamento de Raízes e Método Gráfico

Ver Teoria
Exercício 12345678910

Enunciado

Localize graficamente as raízes das equações a seguir:

a   f x = 4 cos ⁡ x - e 2 x

b   f x = x 2 - t g ( x )

Passo 1

Vamos começar pela letra a .

Ele quer pelo método gráfico, logo, teremos que seguir o passo a passo de sempre.

1ª coisa a se fazer é igualar f x = 0 .

4 cos ⁡ x - e 2 x = 0

4 cos ⁡ x = e 2 x

Beleza! Eu sei o gráfico do cos ⁡ x :

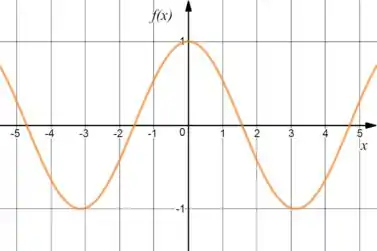
E o do e x :

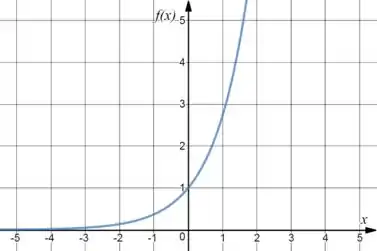
Passo 2

Tá, mas o que eu tenho é h x = 4 c o s ⁡ ( x ) e g x = e 2 x

Em relação ao h ( x ) ele é a mesma função que nós já sabemos, o cosseno, porém com amplitude 4 vezes maior, que vai dar nisso aqui:

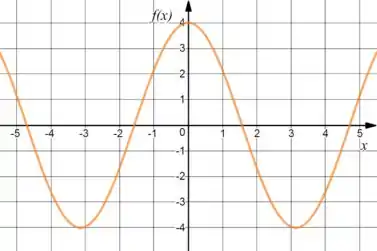
Já no caso do g ( x ) o e x vai aumentar bem mais rápido, logo o gráfico vai dar uma “achatada” pra junto ao eixo. Logo, teremos:

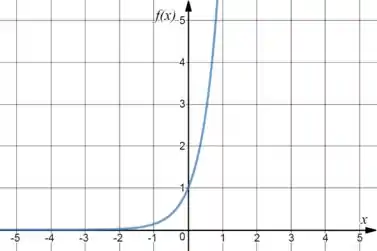
Fazendo a igualdade entre os dois gráficos, vai ficar:

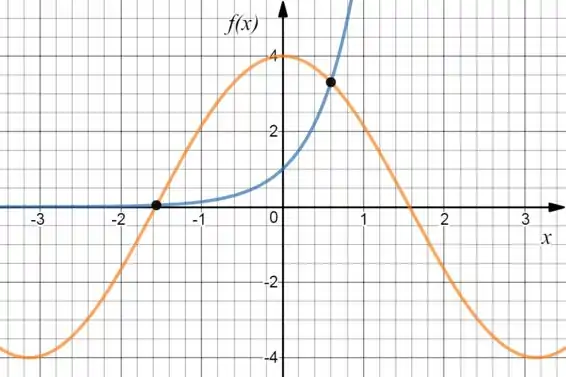
Olhando onde eles se encontram, dá pra estimar mais ou menos as raízes com ξ 1 ≅ - 1 , 6   e   ξ 2 ≅ 0,6 .

Passo 3

Letra b

Fazendo a mesma coisa da letra a , teremos:

f x = 0 = x 2 - t g x

x 2 = t g ( x )

Encontramos h x = x 2 e g x = t g ( x ) .

Uma das raízes está na nossa cara. Pra x = 0 teremos t g x = 0 também, logo ξ 1 = 0 .

A outra raiz vamos ter que juntar os gráficos:

h x = x 2 :

g x = t g x :

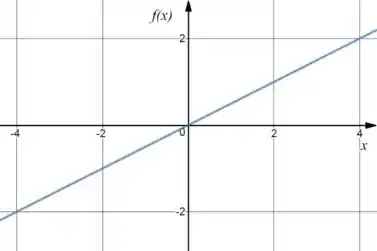
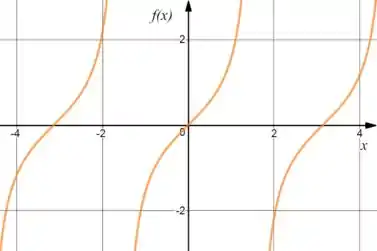
Juntando os dois, teremos:

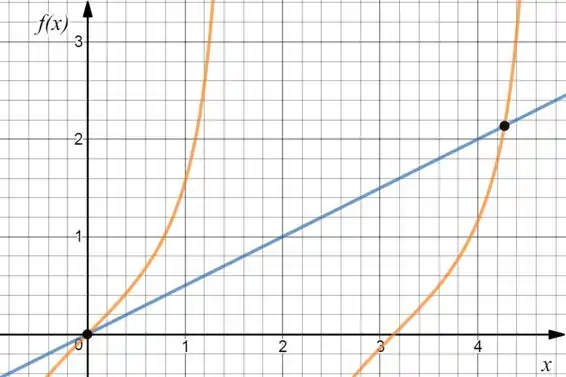
Como podemos ver, uma raiz é o ξ 1 = 0 e a outra está mais ou menos localizada no ξ 2 ≅ 4,2 .

Resposta

  1. ξ 1 ≅ - 1 , 6   e   ξ 2 ≅ 0,6
  2. ξ 1 = 0   e   ξ 2 ≅ 4,2

Exercícios de Livros Relacionados

Localize graficamente as raízes das equações a seguir: 4c o s ( x )-e 2 x=0 x 2 - t g ( x ) = 0 1 - x l n ( x ) = 0 2 x - 3 x = 0 x 3 + x - 1000 = 0
Seja f ( x ) = x + l n ( x ) que possui um zero no intervalo I = [ 0.2,2 ] . Se o objetivo for obter uma aproximação x k para esta raiz de tal forma que | x k - ϵ |1 0 - 5 , é aconselhável usar o méto
Seja f ( x ) = s e n ( x ) - k x . Encontre os valores positivos de k para que f tenha apenas uma raiz estritamente positiva.Encontre os valores positivos de k para que f tenha três raízes estritament
Considere as seguintes funções:a) 𝜓 1 𝑥 =   2 𝑥 − 1   b) 𝜓 2 𝑥 =   𝑥 2 − 2 𝑥   + 2     c) 𝑥 2 − 3 𝑥 + 3 Verifique que 1 é raiz de todas estas funções. Qual delas você escolheria para obter a
Deseja-se obter a raiz positiva da equação: 𝑏 𝑥 2 + 𝑥 − 𝑎 = 0 ,   𝑎0 ,   𝑏0 ,     através do processo iterativo definido por: 𝑥 𝑘 + 1 = 𝑎 − 𝑏 𝑥 𝑘 2 . Qual a condição que devemos impor para