Dada a função , separe-a em duas funções e aproxime pelo menos uma de suas raízes pelo método gráfico.
Passo 1
É! Temos agora uma questão do método gráfico para estimar raízes! Ele nos deu a função . Vamos que vamos buscar a resposta.
Passo 2
O primeiro passo é igualar a função a zero, já que ele quer a raiz, minha .
Passo 3
Opa! Eu sei o gráfico de , certo? É mais ou menos isso aqui:
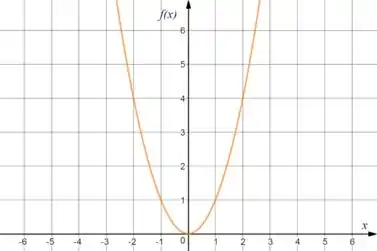
E eu também sei a do . Que é isso aqui:
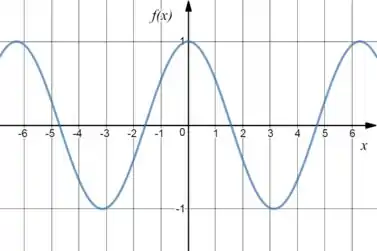
Juntando os dois gráficos, teremos:
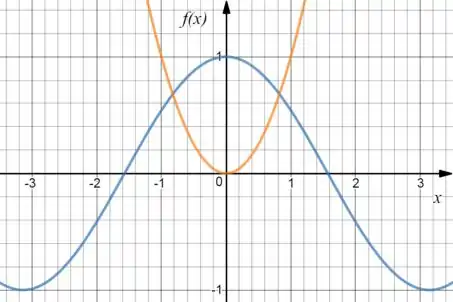
Como ele nos pede apenas uma raiz, escolhendo a raiz positiva, vamos estimar.
Ele está ali pertinho do logo podemos estimar que a raiz é aproximadamente
Resposta
Exercícios de Livros Relacionados
Localize graficamente as raízes das equações a seguir: 4c o s ( x )-e 2 x=0 x 2 - t g ( x ) = 0 1 - x l n ( x ) = 0 2 x - 3 x = 0 x 3 + x - 1000 = 0
Seja f ( x ) = x + l n ( x ) que possui um zero no intervalo I = [ 0.2,2 ] . Se o objetivo for obter uma aproximação x k para esta raiz de tal forma que | x k - ϵ |1 0 - 5 , é aconselhável usar o méto
Seja f ( x ) = s e n ( x ) - k x . Encontre os valores positivos de k para que f tenha apenas uma raiz estritamente positiva.Encontre os valores positivos de k para que f tenha três raízes estritament
Considere as seguintes funções:a) 𝜓 1 𝑥 = 2 𝑥 − 1 b) 𝜓 2 𝑥 = 𝑥 2 − 2 𝑥 + 2 c) 𝑥 2 − 3 𝑥 + 3 Verifique que 1 é raiz de todas estas funções. Qual delas você escolheria para obter a
Deseja-se obter a raiz positiva da equação: 𝑏 𝑥 2 + 𝑥 − 𝑎 = 0 , 𝑎0 , 𝑏0 , através do processo iterativo definido por: 𝑥 𝑘 + 1 = 𝑎 − 𝑏 𝑥 𝑘 2 . Qual a condição que devemos impor para