Ajustar os dados da tabela abaixo por um polinômio do 2º grau completo.
![]()
Passo 1
O professor tá pedindo pra ajustarmos a tabela por um polinômio do 2º grau, então
As funções que multiplicam , , são , e como não temos “nada” ao lado do , podemos dizer também que ele está sendo multiplicado por
Agora precisamos descobrir esses coeficientes , e .
Passo 2
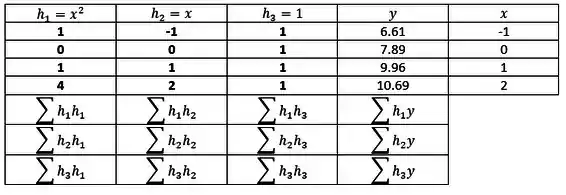
Agora vamos montar a tabela que vai ajudar pacas a aplicar o método.

As colunas e da direita são apenas uma cópia da tabela que o professor deu, blz?
E nas outras 3 colunas a gente coloca as funções que estão multiplicando os coeficientes , e .
A coluna , basta preencher com 1’s. Já a coluna , vai ser preenchida com os valores de , diretinho da tabela que o professor deu. E por último a coluna , será preenchida com os valores de da tabela que o professor deu elevando um a um ao quadrado. Fechow??
Ela vai ficar assim:

Passo 3
Para achar os coeficientes , e vamos fazer o seguinte óh:

Calma, calma é feio, mas é tranquilo de fazer.
Para achar basta multiplicar cada elemento da primeira coluna por ele mesmo e depois soma-los.
Agora vamos achar ou (sim, eles são iguais), pra isso é só multiplicar a primeira coluna pela segunda e somar
Bora achar agora ou (eles também são iguais), pra isso é só multiplicar a primeira coluna pela terceira e somar
Para acharmos é a mesma idéia, só multiplicar os valores da coluna por ela mesma e somar.
Calma tá acabando
Para achar ou (eles também são iguais), pra isso é só multiplicar a segunda coluna pela terceira e somar
E pela última vez, para achar basta multiplicar os valores da coluna por ela mesma e somar.
Uffaaaa! Colocando na tabela temos:
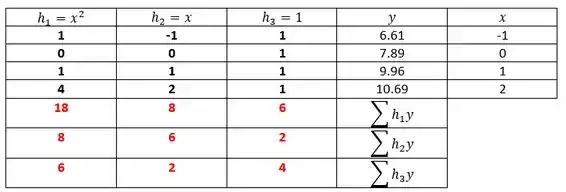
Beleeeeza!!, faltou só multiplicar cada coluna pela coluna do e somar depois. Boora lá!

Passo 4
Se vc já sacou, essa parte de baixo de baixo é um sistema, Ax=b com ele a gente vai encontrar os coeficientes , e
Agora é só resolver o sistema né!!!
Então