Ajuste os dados abaixo pelo método dos mínimos quadrados utilizando:
Uma reta
Uma parábola do tipo
Trace as duas curvas no gráfico de dispersão dos dados. Como você compararia as duas curvas com relação aos dados?

Passo 1
Queremos aproximar a função para uma reta, então o polinômio interpolador será do tipo:
Sabemos que o polinômio será do tipo:
Logo comparando as duas equações concluímos que : e .
Vamos construir os vetores:
- será o vetor com todos os valores de x:
- será o vetor constante pois:
- será o vetor com todos os valores de y:
-
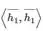
-
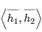
-
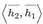
-
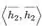
- será o vetor com todos os valores de x² pois :
- será o vetor com valores de x pois:
- será o vetor constante pois:
- será o vetor com todos os valores de y:
Passo 2
Precisamos resolver o seguinte sistema:
![]()
Sendo a matriz , que vai ser já que temos duas funções , como:
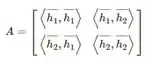
E o vetor :
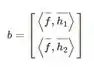
Vamos calcular o termos da matriz A:
Então a matriz é:
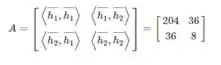
Fazendo as mesmas contas do produto escalar agora para a matriz B, obtemos:
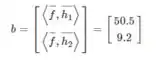
Obtemos agora o sistema:
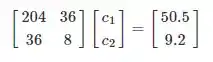
Que nos dá as seguintes equações:
Isolando da segunda equação obtemos:
Substituindo na primeira equação podemos encontrar o valor de e consequentemente :
Com isso, chegamos a resposta:
Passo 3
Agora queremos aproximar para uma parábola, então o polinômio será do tipo:
Sabemos que o polinômio será do tipo:
Logo comparando as duas equações concluímos que :, e .
Temos então os vetores:
Passo 2
Precisamos resolver o seguinte sistema:
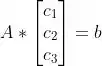
Sendo a matriz :
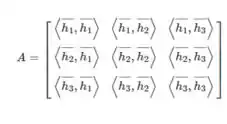
E o vetor :
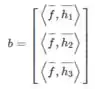
Calculando os termos da matriz A temos:
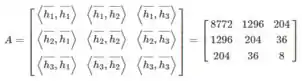
O mesmo para o vetor B:
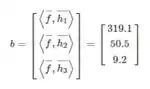
Obtemos o sistema:
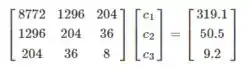
Onde obtemos as seguintes equações:
Resolvendo o sistema obtemos:
Com isso, chegamos a:
Passo 3
Traçando as duas curvas no gráfico de dispersão temos:
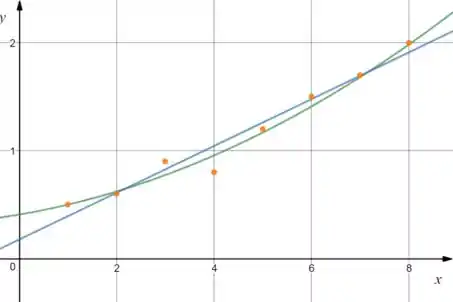
Quando fazemos esse tipo de aproximação, sempre há um erro, se calcularmos qual aproximação tem o melhor erro podemos compará-las. O de resíduo é justamente o erro entre os pontos conhecidos da função e o polinômio interpolador, e é calculado por:
E a mesma fórmula tanto para a reta e para a parábola.
Vamos montar uma tabelinha para cada caso pra ficar mais fácil. Quem tiver a menor soma de resíduos será a melhor interpolação.
Para a reta temos:

E para a parábola:

Logo, temos que o resíduo da parábola é menor, então ela é uma aproximação melhor.
Resposta
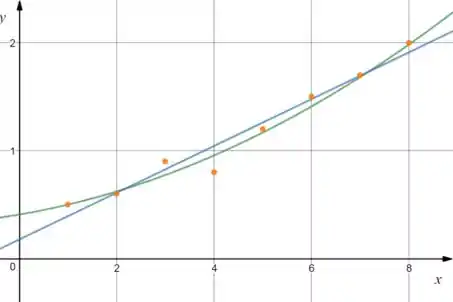
A parábola é a melhor aproximação pois tem um resíduo de enquanto a reta tem um resíduo de .