Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mínimos Quadrados

Ver Teoria
Exercício 612345789101112

Enunciado

Encontre polinômios de grau 1 , 2 e 3 que minimizam o resíduo na aproximação dos dados da tabela abaixo. Qual deles proporcionou um melhor resultado?

Passo 1

Primeira pergunta, o que é esse resíduo? Bom isso aí é só outro nome para aquela soma dos desvios ao quadrado:

∑ k = 1 m f x k - φ x k 2

Passo 2

Vamos começar com o polinômio de primeiro grau! Temos:

φ x = c 1 x + c 2

Logo, h 1 x = x e h 2 x = 1 .

Temos então os vetores:

h 1 ¯ = 0,0.15,0.31,0.5,0.6,0.75

h 2 ¯ = 1,1 , 1,1 , 1,1 , 1

f ¯ = 1,1.04,1.031,1.117,1.223,1.442

Passo 3

Agora montamos a matriz A que vai ser 2 × 2 já que temos duas funções h k x :

A = h 1 ¯ , h 1 ¯ h 1 ¯ , h 2 ¯ h 2 ¯ , h 1 ¯ h 2 ¯ , h 2 ¯ = 1.2911 2.31 2.31 6

E o vetor b :

b = f ¯ , h 1 ¯ f ¯ , h 2 ¯ = 2.849 6.853

Resolvendo o sistema:

1.2911 2.31 2.31 6 c 1 c 2 = 2.849 6.853

c 1 = 0.524

c 2 = 0.940

Com isso, chegamos a:

φ x = 0.524 x + 0.94

Passo 4

Agora vamos calcular o resíduo! Vamos montar uma outra tabelinha pra ajudar a gente:

Então nosso resíduo foi 0.02925 .

Passo 5

Agora o polinômio de segundo grau:

φ x = c 1 x 2 + c 2 x + c 3

Logo, h 1 x = x 2 , h 2 x = x e h 3 x = 1 .

Temos então os vetores:

h 1 ¯ = 0,0.023,0.096,0.25,0.36,0.563

h 2 ¯ = 0,0.15,0.31,0.5,0.6,0.75

h 3 ¯ = 1,1 , 1,1 , 1,1 , 1

f ¯ = 1,1.04,1.031,1.117,1.223,1.442

Passo 6

Agora montamos a matriz A que vai ser 3 × 3 já que temos três funções h k x :

A = h 1 ¯ , h 1 ¯ h 1 ¯ , h 2 ¯ h 1 ¯ , h 3 ¯ h 2 ¯ , h 1 ¯ h 2 ¯ , h 2 ¯ h 2 ¯ , h 3 ¯ h 3 ¯ , h 1 ¯ h 3 ¯ , h 2 ¯ h 3 ¯ , h 3 ¯ = 0.518 0.796 1.291 0.796 1.291 2.310 1.291 2.310 6

E o vetor b :

b = f ¯ , h 1 ¯ f ¯ , h 2 ¯ f ¯ , h 3 ¯ = 1.653 2.849 6.853

Resolvendo o sistema:

0.518 0.796 1.291 0.796 1.291 2.310 1.291 2.310 6 c 1 c 2 c 3 = 1.653 2.849 6.853

c 1 = 1.227

c 2 = - 0.389

c 3 = 1.028

Com isso, chegamos a:

φ x = 1.227 x 2 - 0.389 x + 1.028

Passo 7

Agora vamos calcular o resíduo! Vamos montar aquela mesma tabelinha pra ajudar a gente:

Então nosso resíduo foi 0.003603 .

Passo 8

Por fim, o polinômio de terceiro grau:

φ x = c 1 x 3 + c 2 x 2 + c 3 x + c 4

Logo, h 1 x = x 3 , h 2 x = x 2 , h 3 x = x e h 4 x = 1 .

Temos então os vetores:

h 1 ¯ = ( 0 ,   0.0034 ,   0.0029,0.125,0.216,0.42 )

h 2 ¯ = 0,0.023,0.096,0.25,0.36,0.563

h 3 ¯ = 0,0.15,0.31,0.5,0.6,0.75

h 4 ¯ = 1,1 , 1,1 , 1,1 , 1

f ¯ = 1,1.04,1.031,1.117,1.223,1.442

Passo 9

Agora montamos a matriz A que vai ser 4 × 4 dessa vez já que temos quatro funções h k x . Ô sisteminha chato que vai ficar esse em!

A = h 1 ¯ , h 1 ¯ h 1 ¯ , h 2 ¯ h 1 ¯ , h 3 ¯ h 1 ¯ , h 4 ¯ h 2 ¯ , h 1 ¯ h 2 ¯ , h 2 ¯ h 2 ¯ , h 3 ¯ h 2 ¯ , h 4 ¯ h 3 ¯ , h 1 ¯ h 3 ¯ , h 2 ¯ h 3 ¯ , h 3 ¯ h 3 ¯ , h 4 ¯ h 4 ¯ , h 1 ¯ h 4 ¯ , h 2 ¯ h 4 ¯ , h 3 ¯ h 4 ¯ , h 4 ¯ = 0.241 0.349 0.518 0.796 0.349 0.518 0.796 1.291 0.518 0.796 1.291 2.31 0.796 1.291 2.31 6

E o vetor b :

b = f ¯ , h 1 ¯ f ¯ , h 2 ¯ f ¯ , h 3 ¯ f ¯ , h 4 ¯ = 1.046 1.653 2.849 6.853

Resolvendo o sistema (coragem):

0.241 0.349 0.518 0.796 0.349 0.518 0.796 1.291 0.518 0.796 1.291 2.31 0.796 1.291 2.31 6 c 1 c 2 c 3 c 4 = 1.046 1.653 2.849 6.853

c 1 = 1.379

c 2 = - 0.353

c 3 = 0.061

c 4 = 1.012

Com isso, chegamos a:

φ x = 1.379 x 3 - 0.353 x 2 + 0.061 x + 1.012

Passo 10

Pra encerrar vamos calcular o resíduo montando a tabela:

Então nosso resíduo foi 0.791 × 10 - 3 .

Passo 11

Agora comparamos os resíduos:

Polinômio de grau 1 : 29.25 × 10 - 3

Polinômio de grau 2 : 3.603 × 10 - 3

Polinômio de grau 3 : 0.791 × 10 - 3

O que proporcionou o melhor resultado foi o que teve menor resíduo, o de grau 3 .

Novamente o exercício não pediu isso, mas se liga em como ficaram as curvas:

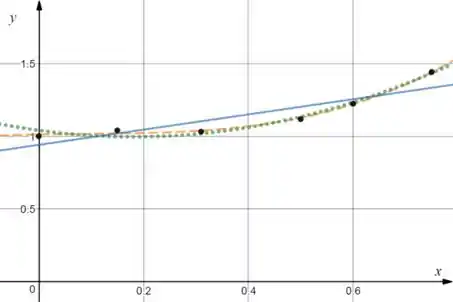
A azul contínua é o polinômio de grau 1 . A verde pontilhada é o polinômio de grau 2 . A laranja tracejada é o polinômio de grau 3 .

Resposta

Grau 1:

φ x = 0.524 x + 0.94

Resíduo: 29.25 × 10 - 3

Grau 2:

φ x = 1.354 x 2 - 0.491 x + 1.04

Resíduo: 3.603 × 10 - 3

Grau 3:

φ x = 1.379 x 3 - 0.353 x 2 + 0.061 x + 1.012

Resíduo: 0.791 × 10 - 3

O polinômio de grau 3 proporcionou o melhor resultado.

Exercícios de Livros Relacionados

Dado um conjunto de valores x k ,f x k ,k = 0,1 , 2 , … , m descreva situações em que você usaria um polinômio interpolador por estes pontos e situações em que você ajustaria uma curva a estes dados p
A tabela abaixo mostra as alturas e pesos de uma amostra de nove homens entre as idades de 25 a 29 anos, extraída ao acaso entre funcionários de uma grande indústria:Faça o diagrama de dispersão dos d
Ajuste os dados abaixo pelo método dos quadrados mínimos utilizando:Um retaUma parábola do tipo a x 2 + b x + c Trace as duas curvas no gráfico de dispersão dos dados. Como você compararia as duas cur
6. Ajuste os dados:a) Usando a aproximação y ≈ 1 / ( a 0 + a 1 x ) . Faça o gráfico para 1 / y e verifique que essa aproximação é viável;b) idem para y = a b x ;c) compare os resultados (a) e (b)
7. O número de bactérias por unidade de volume, existente em uma cultura após x horas é apresentado na tabela:a) Verifique que uma curva para se ajustar ao diagrama é do tipo exponencialb) ajuste aos