Numa pesquisa da Secretaria da Saúde coletou-se N de pessoas infectadas pelo vírus H1N1 num tempo t dado pela tabela abaixo. Admitindo-se que uma reta ajusta os dados da tabela, quantas pessoas estarão infectadas no 2º dia?
![]()
Passo 1
Fala aí, vc decidiu fazer engenharia né? Que que vc tem a ver com H1N1, mas vamo lá né?!
O professor tá pedindo pra ajustarmos a tabela por uma reta, então
Agora precisamos descobrir esses coeficientes e .
A função que acompanha chamaremos de e nesse caso . Podemos dizer também que está sendo multiplicado por
Passo 2
Agora vamos montar a tabela que vai ajudar pacas a aplicar o método

Se liga, a primeira coluna é do , como , basta repetir os valores de dá tabela que o professor deu.
A segunda é a coluna de , e ele é igual a 1. Na última coluna colocamos os valores de diretinho da tabela que o professor deu.
Passo 3
Para achar os coeficientes e vamos fazer o seguinte óh:
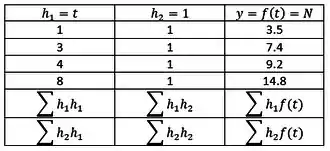
Para achar basta multiplicar cada elemento da primeira coluna por ele mesmo e depois soma-los.
Agora vamos achar ou , pra isso é só multiplicar a primeira coluna pela segunda e somar
Para acharmos é a mesma idéia, só multiplicar os valores da coluna por ela mesma e somar.
Colocando na tabela temos:
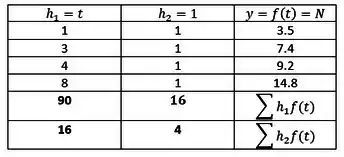
Agora basta achar e , para isso vamos seguir a mesma ideia de multiplicar elemento a elemento as colunas e somar todo mundo.
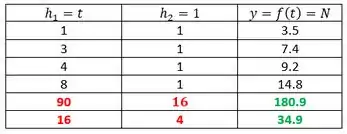
Passo 4
Se vc já sacou, essa parte de baixo de baixo é um sistema, Ax=b com ele a gente vai encontrar os coeficientes e
Agora é só resolver o sistema né!!!
Então
Passo 5
Como o professor quer saber pro 2º dia, basta substituir t=2
Resposta
5.5 milhares de pessoas