Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento de Inércia e Raio de Rotação de Sólidos

Ver Teoria
Exercício 61234578910

Enunciado

  1. Considere o cilindro homogêneo x 2 + y - a 2 ≤ a 2 e 0 ≤ z ≤ h . Calcule o momento de inércia em relação ao eixo z , em função da massa M do cilindro.

Passo 1

Pow, o momento de inércia em relação à z é uma integral tripla, onde

I z = ∭ W x 2 + y 2 ρ x ,   y ,   z d V

Onde já temos a função de densidade ρ x ,   y ,   z = k ( k é a constante de homogeneidade):

k ∭ W x 2 + y 2 d V

Mas aí surge uma duvida:

  • Quem é o sólido W que estamos trabalhando?

Passo 2

Vamos começar aqui respondendo a primeira pergunta!

Então, sabemos que o sólido está delimitado por um cilindro, certo? Porém... Esse cilindro está deslocado de a unidades na direção y , mas ele ainda continua paralelo ao eixo z e mais: como ele tem raio a , ele tangencia o eixo z , veja!

Como 0 ≤ z ≤ h , a altura do cilindro é h !

Passo 3

Pow! estamos dentro de um cilindro, então nada mais justo que pensarmos na mudança para coordenadas cilíndricas, certo?

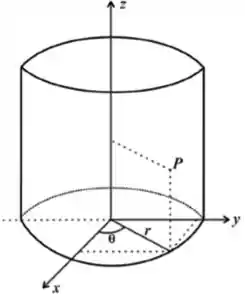
Então troquemos...

x = r cos ⁡ θ  

y = r sin ⁡ θ

z = z

O J a c o b i a n o continua o mesmo

J = r

Ah! E sim, uma equação que ajuda muuuuuito é a equação da própria circunferência:

x 2 + y 2 = r 2

Como sempre, só terminamos uma troca depois que verificamos onde cada um desses novos termo ( r ,   θ   e   z ) variam!

Passo 4

Vamos começar aqui com a variação mais fácil que é a do próprio z . Ora, z varia da base até o topo desse cilindro...

0 ≤ z ≤ h

Em relação ao ângulo θ e ao raio r , bem... Embora o nosso sólido seja esse

fica mais fácil de vermos se desenharmos a projeção do cilindro no plano X Y (a projeção é como se tivéssemos olhando de cima para baixo)

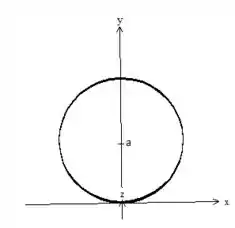
Como o ângulo θ varia sempre saindo do eixo x no sentido anti-horário, observamos que ele precisa variar de uma meia volta

0 ≤ θ ≤ π

Enquanto isso, o r ... Venha comigo !

Passo 5

0 ≤ r ≤ F r o n t e i r a   d o   c i l i n d r o

A fronteira do cilindro é

x 2 + y - a 2 = a 2

Mas poxa, precisamos dessa equação nas novas coordenadas, mas antes... Simplifiquemos isso aí um pouco

x 2 + y - a 2 = a 2           →               x 2 + y 2 - 2 a y + a 2 = a 2         →

  x 2 + y 2 = 2 a y

Substituindo agora...

x 2 + y 2 = 2 a y             →             r 2 = 2 a   r sin ⁡ θ           →

r = 2 a sin ⁡ θ

logo

0 ≤ r ≤ F r o n t e i r a   d o   c i l i n d r o             →

  0 ≤ r ≤ 2 a sin ⁡ θ                                                                                

Passo 6

Bem, agora é só montar a integral tripla e correr para o abraço!

I z = k ∭ W   x 2 + y 2   d V

Lembre-se de substituir pelas coordenadas cilíndricas e não deixar de multiplicar pelo J a c o b i a n o ;)

I z = k ∫ 0 π ∫ 0 2 a sin ⁡ θ ∫ 0 h r 2   J   d z d r d θ

= k ∫ 0 π ∫ 0 2 a sin ⁡ θ ∫ 0 h r 3     d z d r d θ

Integrando a mais interna...

k ∫ 0 π ∫ 0 2 a sin ⁡ θ r 3 ∫ 0 h     d z d r d θ = k ∫ 0 π ∫ 0 2 a sin ⁡ θ r 3 h - 0 d r d θ =

em seguida a do meio...

k h ∫ 0 π ∫ 0 2 a sin ⁡ θ r 3 d r d θ = k h ∫ 0 π r 4 4 0 2 a sin ⁡ θ d θ =

k h ∫ 0 π 2 a sin ⁡ θ 4 4 d θ =

4 k h a 4 ∫ 0 π sin 4 ⁡ θ d θ =

Então, agora preciso que se lembre de que sin 2 ⁡ θ = 1 - cos ⁡ 2 θ 2 ...

4 k h a 4 ∫ 0 π 1 2 - cos ⁡ 2 θ 2 2 d θ =

Fatorando...

4 k h a 4 ∫ 0 π 1 4 - cos ⁡ 2 θ 2 + cos 2 ⁡ 2 θ 4 d θ =

e trocando novamente esse cos 2 ⁡ 2 θ = 1 2 + cos ⁡ 4 θ 2

4 k h a 4 ∫ 0 π 1 4 - cos ⁡ 2 θ 2 + 1 4 1 2 + cos ⁡ 4 θ 2 d θ =

4 k h a 4 ∫ 0 π 1 4 - cos ⁡ 2 θ 2 + 1 8 + cos ⁡ 4 θ 8 d θ = 4 k h a 4 ∫ 0 π 3 8 - cos ⁡ 2 θ 2 + cos ⁡ 4 θ 8 d θ =

chegamos ao resultado...

4 k h a 4 3 8 θ - sin ⁡ 2 θ 2 ∙ 2 + sin ⁡ 4 θ 8 ∙ 4 0 π =

3 2 k h a 4 π

Passo 7

Bem, perceba que estamos buscando a resposta em termos da massa M , correto?

Mas a massa M , a essa altura do campeonato, também é uma integral tripla...

M = ∭ W ρ x ,   y ,   z d V =

Como ρ x ,   y ,   z = k

M = k ∭ W d V = k V o l u m e   d e   W

Como o volume do cilindro é π a 2 h ...

M = k ∭ W d V = k π a 2 h

a resposta em termos da massa é

I z = 3 2 k h a 4 π =

3 2 M a 2

Resposta

3 2 M a 2

Exercícios de Livros Relacionados

Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia de um tijolo retangular com dimensões a ,b e c e massa M se o centro do tijolo está localizado na origem e as arestas
Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia para um cubo com comprimento do lado L se um vértice está localizado na origem e três arestas estão nos eixos coordena
Calcular o momento de inércia do hemisfério x 2 + y 2 + z 2 ≤ 1 ,x ≥ 0 em relação ao eixo y . A densidade no ponto P ( x , y , z ) é proporcional à distância de P ao plano y z .
Calcular o momento de inércia em relação aos eixos coordenados do sólido delimitado por z = 4 - x 2 - y 2 e z = 0 , sabendo que a densidade de massa em um ponto P é proporcional à distância de P ao pl
Calcular o momento de inércia em relação ao eixo dos x do sólido delimitado por z = x 2 + y 2 e z = 4 . A densidade de massa em um ponto P x , y , z é dada por x 2k g / m 3 .