Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento de Inércia e Raio de Rotação de Sólidos

Ver Teoria
Exercício 41235678910

Enunciado

Encontre o momento de inércia em relação ao eixo z do cubo com comprimento do lado 2 , um vértice localizado na origem, três arestas nos eixos coordenados e densidade constante k .

Passo 1

Como sabemos, o momento de inércia de um sólido W em relação ao eixo z é dado por:

I z = ∭ W   x 2 + y 2 ρ ( x , y , z ) d V

Onde ρ ( x , y , z ) é a função densidade. Porém, como o problema diz, a densidade é dada por uma constante k , logo:

I z = k ∭ W   x 2 + y 2 d V

Passo 2

Ótimo, agora vamos escrever matemarticamente essa região.

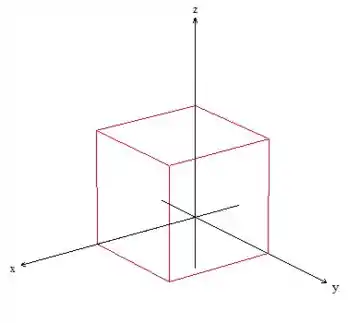
Bom, como se trata de um cubo, não temos muito trabalho para descrever essa região, todos os limites de integração são números:

I z = k ∫ 0 2 ∫ 0 2 ∫ 0 2 x 2 + y 2 d z d x d y

Passo 3

Agora vamos resolver isso aí.

I z = k ∫ 0 2 ∫ 0 2 z x 2 + y 2 0 2 d x d y

I z = 2 k ∫ 0 2 ∫ 0 2 x 2 + y 2 d x d y

I z = 2 k ∫ 0 2 x 3 3 + x y 2 0 2 d y

I z = 2 k ∫ 0 2 8 3 + 2 y 2 d y

I z = 2 k 8 y 3 + 2 y 3 3 0 2

I z = 2 k 16 3 + 16 3

I z = 64 k 3

Resposta

64 k 3

Exercícios de Livros Relacionados

Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia de um tijolo retangular com dimensões a ,b e c e massa M se o centro do tijolo está localizado na origem e as arestas
Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia para um cubo com comprimento do lado L se um vértice está localizado na origem e três arestas estão nos eixos coordena
Calcular o momento de inércia do hemisfério x 2 + y 2 + z 2 ≤ 1 ,x ≥ 0 em relação ao eixo y . A densidade no ponto P ( x , y , z ) é proporcional à distância de P ao plano y z .
Calcular o momento de inércia em relação aos eixos coordenados do sólido delimitado por z = 4 - x 2 - y 2 e z = 0 , sabendo que a densidade de massa em um ponto P é proporcional à distância de P ao pl
Calcular o momento de inércia em relação ao eixo dos x do sólido delimitado por z = x 2 + y 2 e z = 4 . A densidade de massa em um ponto P x , y , z é dada por x 2k g / m 3 .