Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento de Inércia e Raio de Rotação de Sólidos

Ver Teoria
Exercício 91234567810

Enunciado

O momento de inércia relativo ao eixo z do sólido limitado pelo hemisfério cuja equação em coordenadas esféricas é ρ = cos ⁡ ϕ , π 4 ≤ ϕ ≤ π 2 e pelo cone ϕ = π 4 , com densidade constante k , é:

Escolha uma:

a) 2 π k 173

b) π k 320

c) 3 π k 121

d) π k 192

e) π k 312

Passo 1

Cara, o momento de inércia em relação a z é dado pela fórmulinha:

I z = ∫ ∫ ∫ S x 2 + y 2 δ x , y , z d V

Onde δ é a densidade, que o enunciado diz ser

δ = k

E S a região descrita em coordenadas esféricas. Já que estamos com essas coordenadas, vamos passar nossa fórmula para coordenadas esféricas também. Temos que

x = ρ sen ⁡ ϕ cos ⁡ θ ,   y = ρ sen ⁡ ϕ sen ⁡ θ ,   z = ρ cos ⁡ ϕ

x 2 + y 2 + z 2 = ρ 2

J a c = ρ 2 s e n   ϕ

Aí nossa integral fica assim ao aplicar a mudança de variáveis:

I z = ∫ ∫ ∫ S J a c x 2 + y 2 k d V

I z = ∫ ∫ ∫ S ρ 2 s e n   ϕ ρ sen ⁡ ϕ cos ⁡ θ 2 + ρ sen ⁡ ϕ sen ⁡ θ 2 k d V

I z = ∫ ∫ ∫ S ρ 2 s e n   ϕ ρ 2 s e n 2 ϕ cos 2 ⁡ θ + s e n 2   θ k d V

I z = ∫ ∫ ∫ S ρ 2 s e n   ϕ ρ 2 s e n 2 ϕ k d V

I z = ∫ ∫ ∫ S ρ 4 s e n 3   ϕ   k d V

Então a gente precisa calcular essa integral. Bora!

Passo 2

Vamos entender que região é essa que ele descreve, beleza?

Ele começa dizendo que temos um hemisfério (metade de uma esfera) de equação ρ = cos ⁡ ϕ e que está no intervalo π 4 ≤ ϕ ≤ π 2 . Assim é difícil visualizar essa superfície, né?

Para melhorar, podemos tentar passar essa equação para coordenadas cartesianas

ρ = cos ⁡ ϕ

Olha o que acontece se a gente multiplicar os dois lados por ρ :

ρ 2 = ρ cos ⁡ ϕ

Mas a gente sabe que

z = ρ cos ⁡ ϕ

x 2 + y 2 + z 2 = ρ 2

Então

ρ 2 = ρ cos ⁡ ϕ ∴ x 2 + y 2 + z 2 = z

Passo 3

Completando quadrados

x 2 + y 2 + z - 1 2 2 = 1 4

Isso é uma esfera descolocada para cima e de raio 1 2 .

Ela está assim no espaço

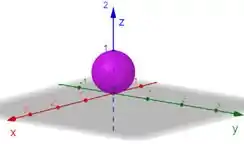
Como ϕ é o ângulo que sai do eixo z , e nosso hemisfério está no intervalo π 4 ≤ ϕ ≤ π 2 , estamos falando do hemisfério de baixo.

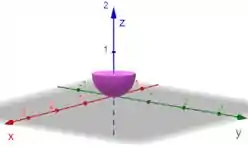
Passo 4

Mas tem um cone nessa história também, o ϕ = π 4 . Que cone é esse?

Cara, esse é o cone que está centrado na origem e que tem essa inclinação. A equação dele é

z = x 2 + y 2

Isso porque só temos a parte de cima do cone, que tem inclinação ϕ = π 4 .

Colocando as duas superfícies num só espaço.

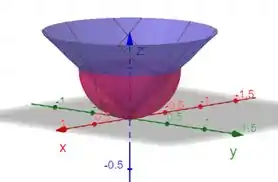
Aí a gente vê que a região fechada S é limitada por cima pelo cone e por baixo pelo hemisfério.

Passo 5

Tudo que a gente precisa fazer é limitar as variáveis das coordenadas esféricas para definir essa região. Repara que a gente já tem algumas coisas do próprio enunciado.

Nossa região está no intervalo

π 4 ≤ ϕ ≤ π 2

Temos que ρ sai da origem e vai até o hemisfério ρ = cos ⁡ ϕ , então

0 ≤ ρ ≤ cos ⁡ ϕ

E como nossa região está em todos os quadrantes de x y (e não temos mais restrições), podemos dizer que

0 ≤ θ ≤ 2 π

Aí nossa integral fica

I z = k ∫ ∫ ∫ S ρ 4 s e n 3   ϕ   d V

I z = k ∫ 0 2 π ∫ π 4 π 2 ∫ 0 cos ⁡ ϕ ρ 4 s e n 3 ϕ d ρ   d ϕ d θ

Passo 6

Agora é calcular essa belezura

I z = k ∫ 0 2 π ∫ π 4 π 2 ρ 5 5   s e n 3 ϕ 0 cos ⁡ ϕ   d ϕ d θ = k 5 ∫ 0 2 π ∫ π 4 π 2 cos 5 ⁡ ϕ   s e n 3 ϕ   d ϕ d θ

Podemos resolver essa integral dessa forma:

Primeiro a gente reescreve s e n 3 ϕ assim:

s e n 3 ϕ = s e n 2 ϕ   s e n   ϕ

Aí a gente lembra que cos 2 ⁡ ϕ + s e n 2 ϕ = 1 ∴ s e n 2 ϕ = 1 - cos 2 ⁡ ϕ .

s e n 3 ϕ = 1 - cos 2 ⁡ ϕ   s e n   ϕ

Nossa integral de dentro fica

∫ π 4 π 2 cos 5 ⁡ ϕ   1 - cos 2 ⁡ ϕ   s e n   ϕ   d ϕ

Aí a gente usa a substituição simples u = cos ⁡ ϕ , e resolve essa belezinha, para achar

I z = k 5 ∫ 0 2 π 5 384 d θ

I z = 2 π k 384 = π k 192

Resposta

Letra d

Exercícios de Livros Relacionados

Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia de um tijolo retangular com dimensões a ,b e c e massa M se o centro do tijolo está localizado na origem e as arestas
Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia para um cubo com comprimento do lado L se um vértice está localizado na origem e três arestas estão nos eixos coordena
Calcular o momento de inércia do hemisfério x 2 + y 2 + z 2 ≤ 1 ,x ≥ 0 em relação ao eixo y . A densidade no ponto P ( x , y , z ) é proporcional à distância de P ao plano y z .
Calcular o momento de inércia em relação aos eixos coordenados do sólido delimitado por z = 4 - x 2 - y 2 e z = 0 , sabendo que a densidade de massa em um ponto P é proporcional à distância de P ao pl
Calcular o momento de inércia em relação ao eixo dos x do sólido delimitado por z = x 2 + y 2 e z = 4 . A densidade de massa em um ponto P x , y , z é dada por x 2k g / m 3 .