Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento de Inércia e Raio de Rotação de Sólidos

Ver Teoria
Exercício 12345678910

Enunciado

Um sólido é limitado abaixo pelo cone z = x 2 + y 2 e acima pelo plano z = 1 . Encontre o raio de rotação desse sólido em relação ao eixo z se a densidade δ ( x , y , z ) = z

Passo 1

Raio de rotação em relação ao eixo z , esse a gente já sabe a fórmula, né?

R z = I z M

Beleza, então precisaremos calcular o momento de inércia I z :

I z = ∭ W x 2 + y 2 δ x , y , z d V

E depois calcular a massa M :

M = ∭ W δ x , y , z d V

Passo 2

Para fazer tudo isso vamos dar uma olhada no gráfico do nosso sólido:

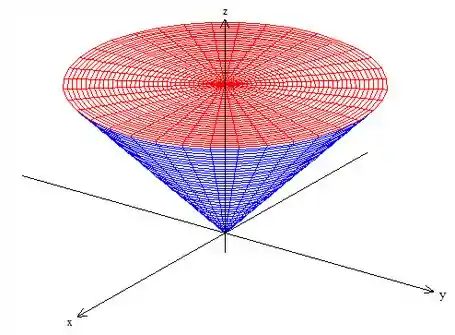
Os limites de z são:

x 2 + y 2 ≤ z ≤ 1

Projetando o sólido no plano x y :

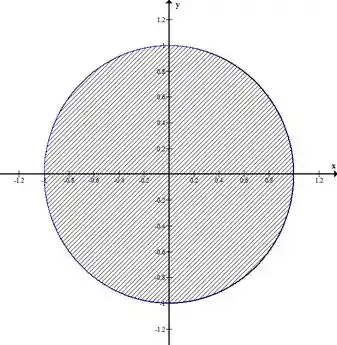
Olhando esses limites no plano xy e a integral do momento de inércia (Lembra que lá tem um x 2 + y 2 também?) dá pra ver que vale a pena fazer uma mudança de coordenada polar, então:

x = r cos ⁡ t

y = r sen ⁡ t

J = r

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

Voltando para os limites de z , também, temos que:

x 2 + y 2 ≤ z ≤ 1

r ≤ z ≤ 1

Passo 3

Jogando esses limites na integral do momento de inércia em relação a z ficamos com:

I z = ∭ W x 2 + y 2 δ x , y , z d V = ∫ 0 2 π ∫ 0 1 ∫ r 1 r 2 z d z r d r d θ

= ∫ 0 2 π ∫ 0 1 r 3 z 2 2 z = r z = 1 d r d θ = ∫ 0 2 π ∫ 0 1 r 3 1 - r 2 2 d r d θ = 1 2 ∫ 0 2 π ∫ 0 1 r 3 - r 5 d r d θ

= 1 2 ∫ 0 2 π r 4 4 - r 6 6 r = 0 r = 1 d θ = 1 2 ∫ 0 2 π 1 4 - 1 6 d θ = 1 2 ∫ 0 2 π 2 24 d θ

= 1 24 . 2 π = π 12

I z = π 12

Passo 4

Calculando a massa do sólido:

M = ∭ W δ x , y , z d V = ∫ 0 2 π ∫ 0 1 ∫ r 1 z d z r d r d θ

= ∫ 0 2 π ∫ 0 1 z 2 2 z = r r = 1 r d r d θ = ∫ 0 2 π ∫ 0 1 1 - r 2 2 r d r d θ = 1 2 ∫ 0 2 π ∫ 0 1 r - r 3 d r d θ

= 1 2 ∫ 0 2 π r 2 2 - r 4 4 r = 0 r = 1 d θ = 1 2 ∫ 0 2 π 1 2 - 1 4 d θ = 1 2 ∫ 0 2 π 1 4 d θ

= 1 8 . 2 π = π 4

M = π 4

Passo 5

Voltando pra nossa fórmula de raio de rotação:

R z = I z M = π 12 π 4 = 1 3

Resposta

1 3

Exercícios de Livros Relacionados

Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia de um tijolo retangular com dimensões a ,b e c e massa M se o centro do tijolo está localizado na origem e as arestas
Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia para um cubo com comprimento do lado L se um vértice está localizado na origem e três arestas estão nos eixos coordena
Calcular o momento de inércia do hemisfério x 2 + y 2 + z 2 ≤ 1 ,x ≥ 0 em relação ao eixo y . A densidade no ponto P ( x , y , z ) é proporcional à distância de P ao plano y z .
Calcular o momento de inércia em relação aos eixos coordenados do sólido delimitado por z = 4 - x 2 - y 2 e z = 0 , sabendo que a densidade de massa em um ponto P é proporcional à distância de P ao pl
Calcular o momento de inércia em relação ao eixo dos x do sólido delimitado por z = x 2 + y 2 e z = 4 . A densidade de massa em um ponto P x , y , z é dada por x 2k g / m 3 .