Calcule o volume do sólido delimitado pelo cilindro , pelo semiespaço e pelos planos e
Dica: usar a mudança de variáveis
Passo 1
Bom, para fazer isso, vamos aplicar uma mudancinha de variáveis como o próprio enunciado nos disse. Façamos
Isso nos da que
Passo 2
Como tivemos uma mudança de varáveis, é necessário que a gente calcule o Jacobiano, certo?
Passo 3
Aplicando então nossas substituições
E o cilindro vai ficar cmomo
Passo 4
Pra encontrar esse volume, aqui que mora o pulo do gato. Sabemos que a altura varia entre 0 e 1, afinal de contas , e lá do enunciado sabemos que varia entre zero e 1.
Sabemos pela equação anterior que encontramos que a base é uma elipse
Onde e
E temos por último do enunciado que , ou seja, . Isso nos da que só queremos a parte acimda de de dentro dessa elipse
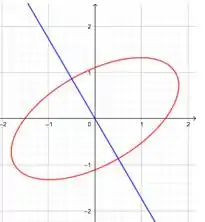
O que é a metade dela. Logo a área será dada por
Para encontrarmos então o volume, multiplicamos pela altura, que no caso é de uma unidade, já que o varia apenas entre 0 e 1. Logo