Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 512346789101112

Enunciado

Utilize a mudança de coordenadas x = u 2 , y = v 2 e z = w 2 para determinar o volume da região delimitada pela superfície x + y + z = 1 e pelos planos coordenados.

Passo 1

Opa, bora la então. Começando fazendo as devidas substituições, oque logo de cara nos leva a ter que u + v + w = 1 . Então agora vamos ver a região que a gente quer determinar o volume.

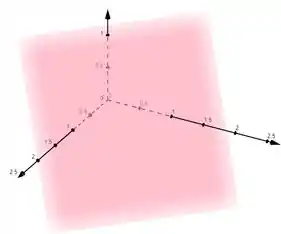
Bom, agora que a gente conhece essa belezinha, tudo fica mais tranquilo. A gente logo vê que todos os valores vao ser positivos, u ≥ 0 ,   v ≥ 0   e   w ≥ 0 , e que u + v + w ≤ 1 .

Passo 2

Calculando agora o Jacobiano, ficamos com:

∂ x , y , z ∂ ( u , v , w ) = 2 u 0 0 0 2 v 0 0 0 2 w = 8 u v w .

Observando no gráfico, vemos que o w varia entre 0 e o plano, que podemos escrever como 1 - u - v , v varia entre 0 e 1 - u , e por ultimo o u varia entre 0 e 1.

Agora falta montar então a integral, resolver e correr pr ao abraço.

Passo 3

Show, como fica nossa integral então?

V = ∫ 0 1 ∫ 0 1 - u ∫ 0 1 - u - v 8 u v w   d w d v d u

4 ∫ 0 1 u ∫ 0 1 - u v 1 - u - v 2   d v d u

4 ∫ 0 1 u 1 - u 2 1 - u 2 2 - 2 1 - u 1 - u 3 3 + 1 - u 4 4 d u

4 ∫ 0 1 u 12 1 - u 4 d u

Fazendo uma substituição simples, 1 - u = p

1 3 ∫ 1 0 1 - p p 4 ( - d t )

1 3 1 5 - 1 6 = 1 90

Resposta

1 90

Exercícios de Livros Relacionados

Calcule ∭ E d V , onde E é o sólido limitado pelo elipsoide x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 Utilize a transformação x = a u , y = b v , z = c w .b) A Terra não é perfeitamente esférica; como resultado
Uma região R no plano x y é dada. Determine equações para a transformaçãoT que mapeia uma região retangularS no plano u v sobre R , onde os lados de S são paralelos aos eixos u e v R é o paralelogramo
Encontre o Jacobiano da transformação. x = 2 u + v , y = 4 u - v
Encontre o Jacobiano da transformação. x = u 2 + u v , y = u v 2