Questão 2: Calcule
Onde é o sólido delimitado pelo elipsoide
Utilize a transformação
Passo 1
Bem, é legal percebermos aqui que buscamos encontrar na verdade um volume já que integral tripla de significa isso por natureza...
Esse é é o nosso elipsoide mesmo...
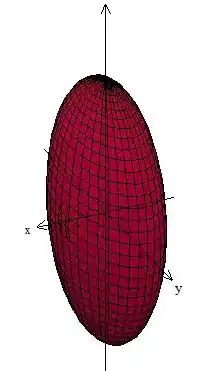
Beleza! Então como vamos calcular esse volume então? Veja que o nosso problema já nos deu uma dica:
“Utilize a transformação , e .”
Então nós iremos fazer uma mudança de variáveis. Você só não deve se confundir aqui com os termos: , e são constantes, enquanto e são as novas variáveis!
Passo 2
Em qualquer mudança, é muito importante aplicar um fator de correção o qual chamamos de Jacobiano aqui:
Calculando essas derivadas...
Calculando o determinante, então chegamos à conclusão de que...
Passo 3
Ok, e qual é a equação que delimita a variação das novas variáveis? Temos que encontra-la também...
OPA! Essa equação em termos das novas variáveis, nos representam uma esfera de raio :
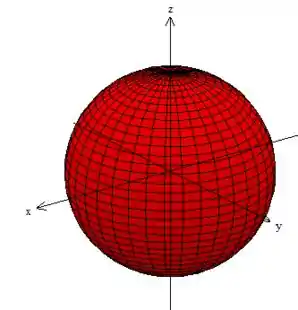
A essa esfera, vamos dar o nome de , ou seja, é a representação da região , mas em termos das novas variáveis da mudança.
Passo 4
Com esses dados em mãos, podemos retornar a integral tripla que estamos calculando:
Veja que em toda mudança devemos trocar a região onde as coordenadas variam () e também não podemos deixar de multiplicar a função que estamos integrando pelo Jacobiano.
Como são constantes...
Como essa integral representa o volume de (uma esfera de raio )...
Logo... Esse é o volume do elipsoide, saca?