Considere as superfícies
- Identifique e esboce
- Identifique e esboce
- Dê uma parametrização da curva espacial
- Ache a equação do plano normal a curva passando pelo ponto
Passo 1
A superfície é dada por
Podemos reorganizar essa expressão da seguinte forma
Que já é algo que nos lembra alguma coisa.
Não? Não te lembra nada?
Então tente pensar que no lugar do tivéssemos um ...
Aí pareceria uma parábola, né?
Pois bem, é isso mesmo! Só que nossa parábola está no “plano” .
Mas na verdade, não temos só uma parábola no plano, porque estamos falando de uma superfície. E superfícies estão em . Assim, nossa parábola vira um cilindro, que tem como geratriz essa parábola.
Passo 2
Na prática, para esboçar, o que precisamos fazer é desenhar essa parábola e “puxar” ela na direção perpendicular ao plano . Assim,
Desenhando a parábola
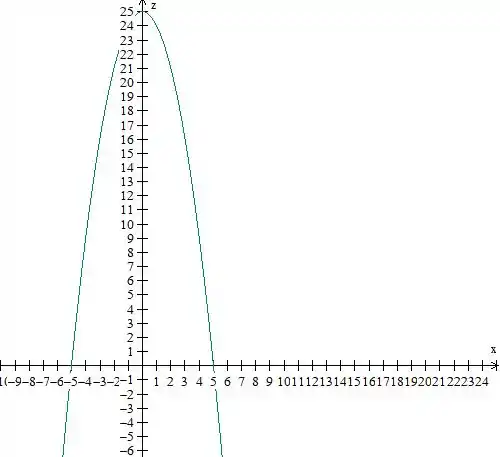
Puxando isso na direção perpendicular ao plano , ou seja, na direção , temos

Passo 3
A superfície é dada por
Que é um paraboloide elíptico, pois podemos escrevê-lo da forma
Veja:
Passo 4
Agora, vamos fazer os traços do paraboloide elíptico. Temos:
- , que é o ponto
- , que é uma parábola no plano , com vértice em
- , que é uma parábola no plano , com vértice em
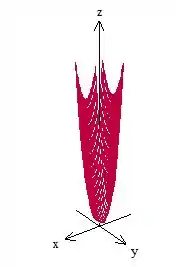
Juntando todas essas informações, vamos ter o seguinte esboço:
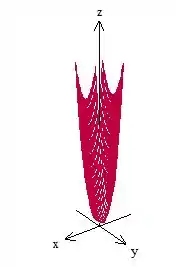
Passo 5
Para fazer uma interseção basta isolar uma variável que as duas equações tenham em comum, e depois igualar os dois resultados.
Na segunda superfície, o já está isolado, ótimo. Então vamos substituí-lo na equação de :
Se dividirmos tudo por , ficamos com
Pronto conseguimos a equação de nossa interseção: uma elipse no plano .
Passo 6
Agora temos que parametrizar a elipse:
Substituindo nossos dados nessa parametrização genérica de uma elipse:
Beleza, agora só falta substituir isso na variável isolada para termos a parametrização completa da nossa curva de interseção (que está no espaço, não se esqueça).
Fazendo isso então, temos
Assim, a parametrização completa da nossa curva é
Passo 7
Agora é fácil. Para encontrar o plano normal a curva no ponto é só seguir o passo a passo:
- Encontrar correspondente ao ponto dado no enunciado ou vice-versa
- Calcular
- Calcular
- Substituir em
Passo 8
Encontrando o valor de :
Igualando as coordenadas, temos
Assim,
Passo 9
Calculando :
No ponto :
Passo 10
A equação do plano normal é então
Ou seja, o plano normal a curva no ponto é o plano .
Resposta

O plano normal a curva no ponto é o plano .