Dada a curva espacial
- Sabendo que a curva espacial está contida em um cilindro sobre uma curva plana:
- Encontre um tempo tal que . Determine um vetor tangente à em e ortogonal à em .
- Escreva a equação cartesiana do plano , ortogonal à no ponto
- Considere a curva espacial
a.1. Determine a equação do cilindro
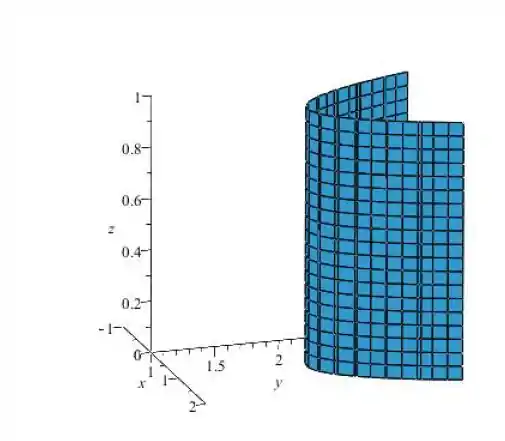
a.2. Esboce
Mostre que e são tangentes no ponto , ou seja, mostre que e se interceptam em e tem o mesmo vetor tangente em . Escreva a equação paramétrica da reta , tangente à e em .
Passo 1
Aqui nós temos que partir da equação paramétrica da curva , achar a equação cartesiana do cilindro .
Para isso, precisamos encontrar uma relação entre o e o .
Vejamos
Assim, temos que
Ou seja
E isso, em é a equação de uma parábola. Mas sabemos que a curva ta contida num cilindro, então, no , essa equação aí representa um cilindro parabólico, ou seja, um cilindro que tem como geratriz, uma parábola, sacou?
Passo 2
Agora que já sabemos quem é o nosso cilindro , que é
Precisamos esboçar ele.
Mas atenção, porque a questão não tá pedindo pra gente esboçar todo o cilindro!
Lembra que o fato de o não aparecer na equação significa que ele pode valer qualquer coisa, oi seja, ele pode variar de menos infinito até mais infinito... Mas aí a questão pediu pra gente desenhar o cilindro limitando o , apenas entre e .
Assim, desenhando nossa parábola no plano ( onde ) e “subindo” com ela até onde , temos
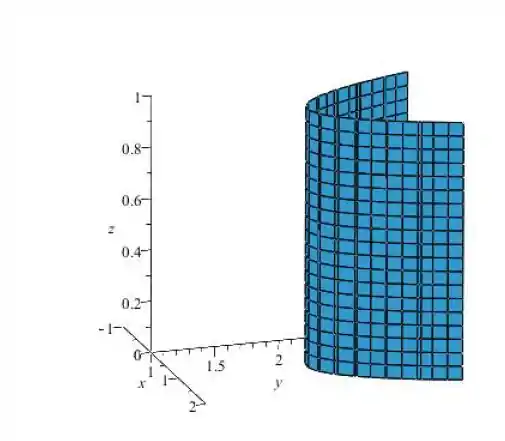
Passo 3
Precisamos fazer
Assim
Igualando as coordenadas, a gente tira que
Passo 4
Beleza, agora precisamos de um vetor tangente ao cilindro da letra e perpendicular ao vetor .
Vamos descobrir quem é esse tal de então, né?!
Assim, no ponto :
Passo 5
Ok, mas mais do que saber quem é esse vetor, precisamos entender ele.
Como ele é o vetor derivada da curva , então ele é um vetor tangente à .
Ora, mas se ta contida no cilindro, então esse vetor também é tangente ao cilindro.
Então quer dizer que já achamos o que a questão pediu pra gente?
Na verdade, não
Porque a questão quer um vetor que seja tangente ao cilindro E perpendicular a . Então, não serve, porque ele não pode ser perpendicular a ele mesmo, né?
E agora, como a gente vai descobrir esse vetor então?
Pensa comigo: se fizermos um produto vetorial entre um vetor normal ao cilindro e esse vetor tangente ao cilindro, vamos encontrar um vetor que é, simultaneamente, perpendicular a esses dois vetores.
E, com a regra da mão direita, você pode ver que esse vetor vai ser exatamente o vetor que estamos procurando, isto é, um vetor tangente ao cilindro, mas ao mesmo tempo, perpendicular ao outro vetor tangente ao cilindro.
Ótimo, então agora nosso problema tá em encontrar um vetor normal ao cilindro, pra podermos fazer o produto vetorial
Ora, mas isso não é um problema, porque todo mundo já tá careca de saber que o vetor gradiente é perpendicular a uma superfície que é gráfico de uma função.
Assim, se definirmos a função
Que é a função cujo gráfico é o cilindro , temos o vetor gradiente
No ponto :
Passo 6
Agora sim, podemos finalmente fazer o produto vetorial para encontramos o vetor que estamos procurando:
Passo 7
Agora vamos ao plano normal a no ponto .
Se estamos procurando o plano normal a curva, precisamos de um vetor normal ao plano, que no caso, será um vetor tangente a curva.
E esse vetor tangente a curva nós já temos, que é o vetor
Que, inclusive, já está calculado no valor do parâmetro correspondente ao ponto de tangencia .
Então, só falta mesmo a gente substituir tudo na equação do plano:
É o nosso plano .
Passo 8
Agora precisamos mostrar que e :
- Se interceptam em
- Tem o mesmo vetor tangente em .
Pra mostrar o item , é só a gente mostrar que as duas curvas passam pelo ponto , não necessariamente no mesmo instante .
Já sabemos que passa por quando , pois
Agora, vamos fazer
Daí, igualando as coordenadas, tiramos que
“uéeee, mas não era igual a ???”
Calma jovem, muita calma nessa hora! O valor é o valor do parâmetro da curva correspondente ao ponto . O valor é o valor do parâmetro da curva correspondente ao ponto . Embora seja a mesma letra, eles são parâmetros de curvas diferentes.
Beleza, então, como conseguimos encontrar um valor de tanto pra curva quanto pra curva , então já provamos o primeiro ponto.
Passo 9
Vamos ao segundo ponto então.
Temos que provar que as duas curvas tem o mesmo vetor tangente em .
O vetor tangente de em nós já achamos no passo 4:
Agora precisamos achar um vetor tangente pra e ver se ele é o mesmo vetor aí de cima.
No ponto , que corresponde a :
Ebaaaa, então
Provamos o segundo ponto também!
Passo 10
Agora, pra encerrar de vez essa questão, vamos só escrever a equação da reta tangente a e em .
Já temos o ponto de tangencia e o vetor tangente, logo:
Resposta