Os fios e são feitos de materiais diferentes e têm comprimentos .
A resistividade e o diâmetro do fio são e , e a resistividade e o diâmetro do fio são e .
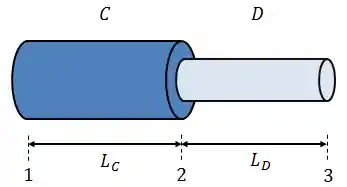
Os fios são unidos da forma mostrada na figura abaixo, e são submetidos a uma corrente de . Use .
- Calcule as densidades de corrente nos fios e .
- Calcule o módulo do campo elétrico no interior do fio e no interior do fio .
- Determine a diferença de potencial entre os ponto e , e entre os pontos e .
- Determine a potência dissipada entre os pontos e , e entre os pontos e .
Passo 1
a) Calcule as densidades de corrente nos fios e .
Vambora!
A densidade de corrente, por definição, é dada por:
Onde corresponde à corrente e corresponde à área da seção transversal.
Nesse caso, como a seção transversal é uma circunferência, ... só que como o problema tá falando dos diâmetros desses caras, podemos dizer que:
Em que é o diâmetro desse cara.
Agora sim!
Partiu!
Passo 2
b) Calcule o módulo do campo elétrico no interior do fio e no interior do fio .
Opa! Tá bonito, hein!
Agora que acabamos de calcular a densidade de corrente nos dois fios, podemos encontrar o campo elétrico no interior de cada um através da relação:
Onde:
Agora já podemos brincar.
Passo 3
c) Determine a diferença de potencial entre os ponto e , e entre os pontos e .
Tem dois caminhos pra resolver esses caras.. o primeiro, e mais trabalhosa, é usar a relação:
e calcular a resistência de cada fio.
O segundo, e mais tranquilo, é basicamente usar a equação:
Só isso? Sim, só isso... onde .
Passo 4
d) Determine a potência dissipada entre os pontos e , e entre os pontos e .
Existem três fórmulas para calcular a potência dissipada em um resistor:
Nesse caso, já que já calculamos as diferenças de potencial, vai ser mais jogo para nós se usarmos a primeira relação:
Resposta
a.
b.
c.
d.