O consumo médio de gasolina em um certo tipo de automóvel é de , segundo informações da montadora. Uma revista especializada verificou o consumo em desses veículos, escolhidos ao acaso, e constatou consumo médio de . Admita que o consumo siga o modelo normal com variância igual a . Considere nível de significância de 10% para os testes abaixo.

(b) Teste a afirmação da montadora de que a média de consumo é igual a contra a alternativa de ser diferente de .

Letra b)

Aqui temos o nosso clássico teste bilateral, o de sempre. Vamos às hipóteses:

Nosso continua o mesmo, afinal nossos parâmetros não mudaram:

E nossa agora é um pouquinho diferente, é aquela que calculamos dois ! Desse jeitinho aqui ó:

também não aparece na tabela. Usamos o , que é suficientemente próximo de !

Nossa vai ser então a parte azul da gaussiana:

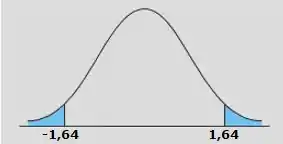
Agora resta ver se nosso tá dentro ou fora dessa região:

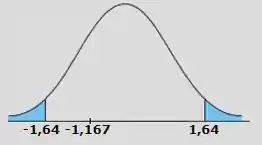
Tá fora!!! Então não rejeitamos , em outras palavras, não se rejeita a hipótese de que nossa média populacional seja igual a !