Exercícios Resolvidos de Teste de Hipóteses para Média Populacional com σ Conhecido
Ver TeoriaEnunciado
O responsável pelo controle de qualidade de uma fábrica que vende suco de laranja, supervisiona periodicamente a linha de produção, para verificar se as caixas de suco de laranja estão com a quantidade correta de suco, isto é, verifica se não está ocorrendo sobreenchimento ou subenchimento da caixinha. Em média, o volume das caixas de suco é de litro e o desvio padrão populacional é de litro. Para testar a hipótese de que haja a necessidade de recalibrar a máquina que enche as caixas, foi retirada uma amostra de caixas de suco. A média encontrada foi de litro. Ao nível de significância de , teste as hipóteses e diga sua conclusão.
Passo 1
Primeiro construímos as hipóteses:
É diferente por que queremos testar se existe sobreenchimento ou subenchimento de suco, então estamos num teste bilateral!
Passo 2
Calculamos nossa estatística de teste:
Passo 3
Agora calculamos nossos pontos críticos (lembrando que nosso ), que no teste bilateral são:
Então nossa região crítica é tudo que tá na região azul:
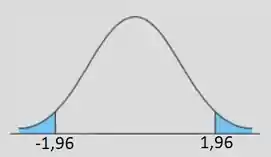
Como nossa estatística de teste que vale está nela, nós rejeitamos a hipótese nula!
Resposta
Rejeita-se .