Exercícios Resolvidos de Teste de Hipóteses para Média Populacional com σ Conhecido
Ver TeoriaEnunciado
Probabilidade e Estatística – PUC RJ – 2019.1 – P4 – Questão 6
Foi obtida uma amostra de 30 botas usadas por soldados em uma operação numa região de deserto e apresentou uma vida média de 1,24 anos e desvio padrão de 0,55 anos. Por outro lado, em situações normais o tempo médio de vida nominal destas botas é 1,40 anos.
Podemos afirmar ao nível de significância de 5% que a utilização destas botas no deserto diminui o seu tempo de vida?
(Mostre os resultados através do cálculo da estatística do teste.)
Passo 1
Bom, esse é um problema típico de teste de hipótese. O primeiro passo em qualquer problema desse tipo é definir as hipóteses.
Nossas hipóteses são: o tempo de vida médio é o mesmo apesar do usa na operação no deserto (hipótese nula) ou o tempo de vida médio diminui com o uso na operação (hipótese alternativa).
Trata-se de um teste unilateral à esquerda pois a limitação da hipótese alternativa restringe nossa análise para uma região à esquerda de . Se a hipótese alternativa fosse , aí o teste seria unilateral à direita.
Para fazer o teste, temos que calcular o desvio padrão da média que é o desvio padrão amostral dividido pela raiz quadrada de :
Passo 2
Para fazer esse tipo de teste nós vamos usar a distribuição de Student com a variável
Essa variável segue uma distribuição de Student com graus de liberdade. A seguir faço um esboço da situação:
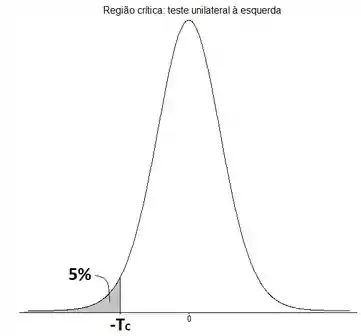
Queremos descobrir o valor de tal que , que corresponde a região crítica do teste. Como a distribuição é simétrica, temos que
Para achar o valor de temos que olhar para a tabela dessa distribuição na linha correspondente a graus de liberdade:
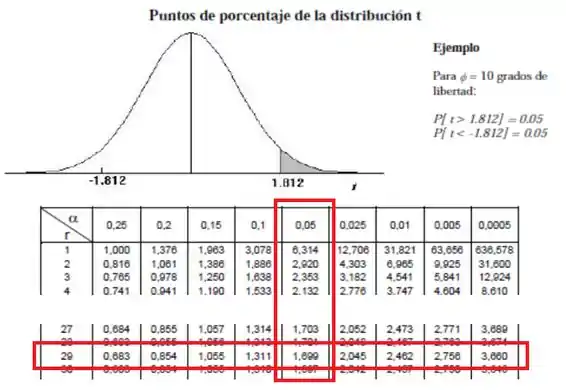
Nós achamos que
Passo 3
Agora vamos interpretar esse resultado para finalizar o teste de hipótese!
A hipótese deve ser rejeitada se . Isso significa que
Multiplicando a inequação por :
Portanto,
Isso significa que a região de rejeição de é dada por valores de menores que . Caso isso aconteça, podemos rejeitar a hipótese . Nesse caso, vimos no passo 1 que , de modo que a condição para rejeição de não é satisfeita!
Isso significa que não podemos descartar, via teste estatístico, a hipótese de que a média dos tempos de vida é compatível com o valor de referência. Portanto, não podemos garantir com a significância de 5% que o tempo de vida médio das botas diminui com o uso, pois estatisticamente ele é compatível com a referência de anos.
Resposta
Não.