Exercícios Resolvidos de Teste de Hipóteses para Média Populacional com σ Conhecido
Ver TeoriaEnunciado
TAREFA da aula – 10 – Probabilidade e Estatística (ENG1029) – 2020/2 – Questão 2
Você é dono de uma empresa construtora e seleciona aleatoriamente casas construídas recentemente. A média amostral do custo de construção é de e do desvio padrão amostral é de . Assumindo que os custos com a construção são normalmente distribuídos, pede-se:
a) Testar ao nível de significância de a hipótese nula do verdadeiro custo médio de construção ser
b) Testar ao nível de significância de a hipótese nula do verdadeiro desvio padrão de construção ser
Passo 1
a) Bora pra segunda questão dessa nossa última lista, galerinha!
Bem! As nossas hipóteses são:
Por isso, primeiro calculamos a estatística de teste (lembrando que não conhecemos o desvio padrão populacional):
Passo 2
Passo 3
Nossos pontos críticos são dados por:
Lembrando que e , podemos procurar esse cara na tabela :
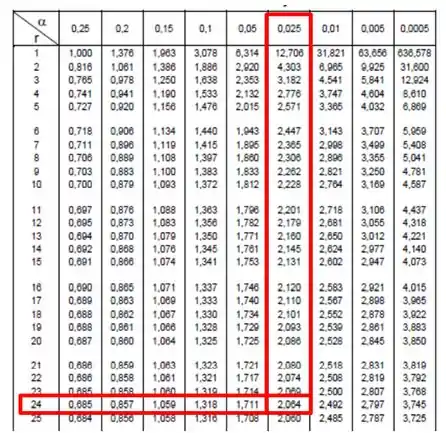
Sendo assim, temos que...
Passo 4
Portanto nosso gráfico fica:
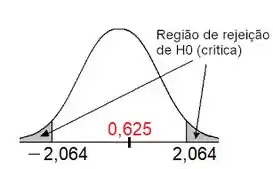
Então não podemos rejeitar a hipótese nula, pois a estatística de teste cai fora da região crítica . A média pode, portanto, ser igual a .
Passo 5
b) Agora, vamos testar ao nível de significância de a hipótese nula do verdadeiro desvio padrão de construção ser
Presta atenção! Se o desvio padrão é , então a variância vai valer...
Construindo nossas hipóteses:
Calculando a estatística de teste:
Passo 6
Nossos pontos críticos para o teste Qui-Quadrado no caso Bilateral são:
Onde . E como o nível de significância pedido foi de , :
Olhando a tabela...
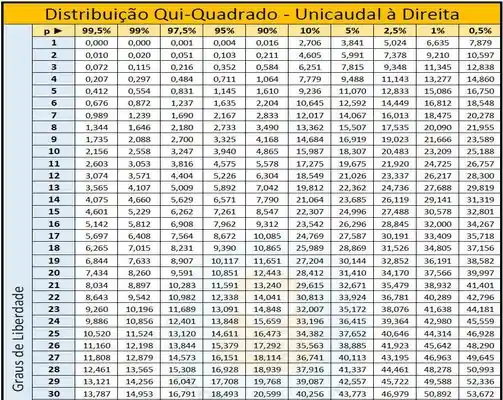
Temos que...
Como...
Isso significa que nossa estatística de teste cai fora da região crítica , então não podemos rejeitar a hipótese nula. Ou seja, nosso desvio padrão populacional pode ser igual a .
Resposta
a) Não rejeita-se . A média pode ser igual a .
b) Não rejeita-se . O desvio padrão populacional pode ser igual a .