O consumo médio de gasolina em um certo tipo de automóvel é de , segundo informações da montadora. Uma revista especializada verificou o consumo em desses veículos, escolhidos ao acaso, e constatou consumo médio de . Admita que o consumo siga o modelo normal com variância igual a . Considere nível de significância de 10% para os testes abaixo.

(a) Teste a afirmação da montadora de que a média de consumo é igual a contra a alternativa de ser igual a .

Vamos calcular nossa estatística de teste, como sempre fizemos, que é esse cara aqui:

Lembrando que no enunciado nos foi dado:

Ou seja, todas as incógnitas que entram no nosso . Então temos que:

Agora temos que calcular nossa região crítica, ou seja, a região que rejeitamos . Mas eu uso a fórmula do teste unilateral inferior ou superior?

Repara comigo: nossa hipótese alternativa testa um valor menor que o valor testado pela hipótese nula, certo? Por isso, nós vamos poder usar o teste unilateral inferior aqui! Se quiséssemos testar um valor maior que o da hipótese nula, usaríamos o superior.

E para o teste unilateral inferior, procuramos na tabela da Normal. Para isso, precisamos descobrir quem é ! O enunciando nos diz que para considerar um nível de significância de 10%, entããão:

Daí tiramos que:

E procurando esse cara no corpo da tabela, temos que:

não aparece na tabela, então pegamos o , que era o mais próximo!

Então nossa região crítica vai ser a parte azul da gaussiana:

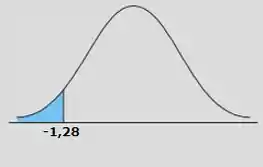
Agora vemos se nosso tá dentro ou fora dela:

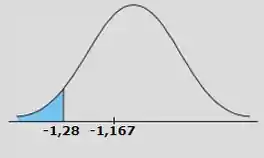
Tá fora!!! Então não rejeitamos , ou seja, não se rejeita a hipótese de que nossa média populacional seja igual a !