Funcionários de uma grande firma de contabilidade afirmam que a média dos salários dos contadores é menor que a de seu concorrente, que é . Uma amostra aleatório de contadores da firma mostrou que a média dos salários de . Sabe-se, de estudos anteriores, que o desvio padrão dos salários é de . Teste a afirmação dos funcionários ao nível de de significância.

Calculamos nossa estatística de teste:

Agora calculamos nosso ponto crítico (lembrando que nosso ), que no teste unilateral inferior é:

Fizemos esse arredondamento por que é o mais aproximado de na tabela que usamos! Com esse ponto crítico, temos que nossa região crítica vai ser:

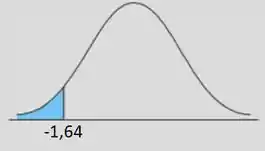
Como nossa estatística de teste tá caindo FORA dessa região aí, nós NÃO rejeitamos a hipótese nula!