Exercícios Resolvidos de Teste de Hipóteses para Média Populacional com σ Conhecido
Ver TeoriaEnunciado
Probabilidade e Estatística – PUC RJ – 2019.2 – P3 – Questão 5
Um revendedor de baterias recebeu um grande carregamento de um fabricante que afirma que as baterias têm uma vida média de 1200 horas. Uma amostra com 10 baterias extraída deste carregamento apresentou média amostral de 1280 horas e . Os dados indicam que a vida média das baterias recebidas é maior do que as 1200 horas anunciadas?
(Realize o teste com 1% de nível de significância.)
Passo 1
Esse é um exercício clássico sobre teste de hipótese. Queremos discutir estatisticamente se a vida média das baterias é maior que 1200 horas ou não.
Para isso, vamos primeiro achar a média e o desvio padrão da média associado a amostra de 10 baterias mencionada no problema. A média é
O desvio padrão da média é
Passo 2
Para resolver esse problema, vamos usar o teste T. Mas antes disso, vamos definir as hipóteses:
Trata-se de um teste unilateral à direita.
A variável de Student é dada por
Essa variável segue uma distribuição de Student, cuja distribuição eu mostro a seguir:
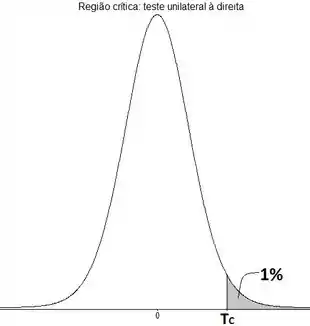
Vamos obter o valor de tal que
Para isso, vamos olhar para a tabela na linha graus de liberdade:
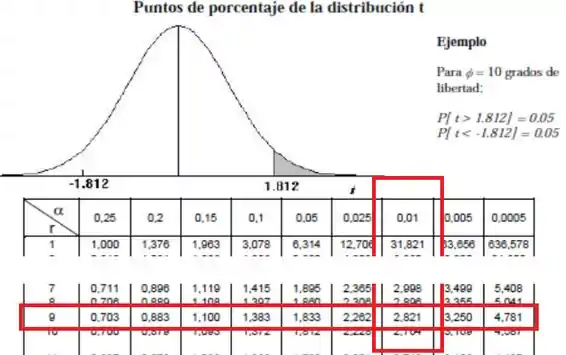
Tiramos que
Passo 3
Nós devemos rejeitar se
Mas sabemos que
Assim, devemos rejeitar se
Caso essa condição não seja satisfeita, não podemos descartar . No passo 1 vimos que . É fácil ver que a condição não é satisfeita, de modo que não podemos descartar . Como essa hipótese estabelecia que , não podemos descartar que a média é 1200.
Isso significa que não podemos afirmar estatisticamente que a o tempo de vida médio das baterias é maior que 1200 horas. Para que rejeitássemos e pudéssemos falar que a média é superior a 1200, deveríamos ter .
Resposta
Não podemos afirmar.