Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transferência de Calor

Ver Teoria
Exercício 6312345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626465666768697071727374757677787980818283848586878889

Enunciado

UFPE – Física 2 – 2020.2 – P6 – Discursiva

1 . Considere um recipiente com paredes feitas de um material isolante (adiabáticas) exceto pela base, que é feita de material condutor térmico, tem espessura L = 20   c m , área de secção transversal A = 0,33   m 2 e coeficiente de condutividade térmica k = 200   W / ( m ⋅ K ) .

Dentro deste recipiente há 1,0   k g de gelo fundente a 0,0   ° C . O recipiente está sobre uma base térmica (reservatório térmico) que está a uma temperatura constante de 10,0   ° C , como mostra a figura.

(Considere L f = 330   k J / k g ; c á g u a = 4,2   k J / k g   ° C ).

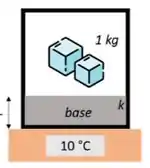
Baseado nessas informações, analise as afirmações e marque a alternativa correta.

I ) O gelo será transformado totalmente em água em aproximadamente 1 minuto e 40 segundos

I I ) Após a transformação, o sistema atinge a temperatura de equilíbrio a 5 ° C

I I I ) A quantidade de calor necessária para transformar totalmente o gelo em água a 10   ° C é de 372   k J

a ) somente I I é verdadeira

b ) somente I I e I I I são verdadeiras

c ) Somente I é verdadeira

d ) Somente I e I I I são verdadeiras

e ) todas são verdadeiras

Passo 1

Vamos falar com calma sobre cada uma das afirmações.

I - Sabemos que:

P = Q Δ t

E é esse Δ t que queremos descobrir.

Por outro lado, também conhecemos a equação dada por:

P = k A Δ T L

Então vamos igualar as duas coisas e ver se chegamos ao valor presente na afirmação.

k A Δ T L = Q Δ t ⇒ Δ t = Q L k A Δ T

Temos quase todas as informações menos Q , o que podemos fazer?

Bom, Q = m L F e o enunciado nos dar essas informações então substituindo os valores que o enunciado nos deu temos:

Δ t = 1   k g 330 ⋅ 10 3   J / k g 20 ⋅ 10 - 2 m ( 200   W / ( m ⋅ K ) ) ( 0,33   m 2 ) ( 10   K ) = 100 s

Δ t = 1   m i n u t o   e   40   s e g u n d o s

A afirmação I é verdadeiro e isso significa que podemos excluir os itens a ) e b ) .

Passo 2

I I - Bom, já podemos dizer que essa afirmação é falsa pois é dito no enunciado que a base tem uma temperatura constante de 10,0   ° C e o sistema entrará em equilíbrio quando tiver a mesma temperatura da base, ou seja, afirmação falsa e já podemos excluir o item e ) .

Estamos quase lá, bora pra última afirmação

Passo 3

I I I - Para isso vamos usar a equaçãozinha:

Q t o t a l = Q f u s ã o + Q 0 ° C → 10 ° C

Ou seja:

Q t o t a l = ( 1   k g ⋅ 330 ⋅ 10 3   J / k g ) + ( 1 k g ⋅ 4,2   k J / k g   ° C ⋅ 10   ° C )   = 330   k J + 42   k J = 372   k J

Verdadeira também!

Então a resposta correta é o item d ) .

Resposta

d ) Somente I e I I I são verdadeiras

Exercícios de Livros Relacionados

O álcool etílico tem um ponto de ebulição de 78 ° C , um ponto de congelamento de - 114 ° C , um calor de vaporização de 879 k J / k g , um calor de fusão de 109 k J / k g , e um calor específico de 2
Que massa de vapor a 100 ° C deve ser misturada a 150 g de gelo no ponto de fusão, em um recipiente isolado termicamente, para produzir água a 50 ° C .
Que massa de manteiga, que possui um valor calórico de 6,00 C a l / g( 6000 c a l / g ) , equivale à variação d energia potencial gravitacional de um homem de 73 k g que sobe do nível do mar para o al
Uma substância tem massa de 5 0 , 0 g / m o l . Quando 314 J são adicionados na forma de calor a uma amostra de 30 g da substância, a temperatura sobe de 25 ° C para 45 ° C . a Qual é o calor específi
Um termômetro com 0,0550k g de massa e um calor específico de 0,837 k J K g . K indica 15,0° C . O termômetro é totalmente imerso em 0,300k g de água por tempo suficiente para ficar à mesma temperatur