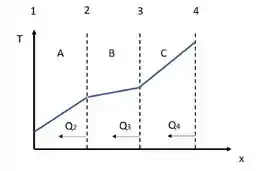
Uma parede composta de três camadas (de mesma espessura) de materiais A, B e C separa dois reservatórios térmicos com temperaturas e . No regime estacionário, o perfil de temperatura na parede pode ser representado pela figura. Sabendo que , e representam as quantidades de calor que passam através das interfaces indicadas na figura, , e são as condutividades térmicas dos materiais e e as temperaturas nas interfaces 2 e 3, podemos escrever que:
(a) , e
(b) , e
(c) , e
(d) , e
(e) , e
(f) , e
Passo 1
Essa questão foi anulada! Porque não tinha resposta. Kkkkkk Mas vamos fazer pra achar a nossa resposta e pra você saber tuuuudo na hora da prova.
Então, como é uma parede de camadas, o fluxo de calor vai ser o mesmo nas 3 camadas. Ou seja:
A temperatura diminui de 4 pra 1. Então:
Os fluxos de calor vão ser:
Como é uma parede a área A vai ser a mesma pras três camadas. E nos foi dito que a espessura l também é a mesma, então:
Como:
E:
Então:
E a resposta seria:
, e
Resposta
, e