Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Valores Médios em Sólidos

Ver Teoria
Exercício 9123456781011

Enunciado

UFF, Volta Redonda, Cálculo Diferencial e Integral II, Listas Cálculo Diferencial e Integral II - Lista 2 - Integral Tripla - 2019.1, Questão 4.

4-Calcule a massa do sólido limitado pelo paraboloide z = x 2 + y 2 e pelo plano z = 4 , sendo a densidade em cada ponto do sólido dada por σ x , y , z = x 2 + y 2

Passo 1

Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nesse problema estamos interessados em obter a massa do solido limitado pelas curvas z = x 2 + y 2 e z = 4 cuja densidade volumétrica é dada por σ x , y , z = x 2 + y 2 .

Tem ideia do que podemos fazer? 🤔

A primeira coisa é analisar o sólido entre z = x 2 + y 2 e z = 4 . Já adianto que nesse problema vamos usar simetrias cilíndricas para resolver o problema.

Nesses casos convertemos x para r c o s θ e y para r s e n θ e na integral, acrescentamos o jacobiano r .

Como estamos interessados na massa, multiplicamos a função de integração pela densidade volumétrica σ x , y , z .

Sacou? Bora começar! 😉

Passo 2

Analisando o solido de integração, temos

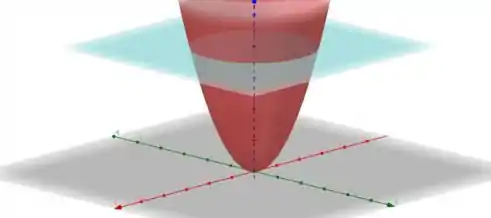
Assim, vemos que a simétrica cilíndrica vai nos ajudar a obter a resposta.

Montando a integral, temos que em z o solido varia de z = x 2 + y 2 até z = 4 . O raio é obtido igualando z nas equações z = x 2 + y 2 e z = 4 , obtendo 0 ≤ r ≤ 2 e por fim, a variação angular de 0 a 2 π

∫ 0 2 π ∫ 0 2 ∫ x 2 + y 2 4 σ x , y , z d z r d r d θ

Como σ x , y , z não depende de z , a integral com relação a z é

∫ x 2 + y 2 4 σ x , y , z d z = σ x , y , z 4 - x 2 + y 2

Convertendo o resultado para as coordenadas cilíndricas, temos

σ x , y , z = x 2 + y 2 → σ r , θ , z = r

4 - x 2 + y 2 → 4 - r 2

Substituindo na integral...

∫ 0 2 π ∫ 0 2 r · r 4 - r 2 d r d θ

∫ 0 2 π ∫ 0 2 4 r 2 - r 4 d r d θ

Tranquilo até aqui? 👀

Passo 3

Integrando pelo método de integração polinomial com relação a r ...

∫ 4 r 2 - r 4 d r = 4 r 2 + 1 2 + 1 - r 4 + 1 4 + 1 = 4 r 3 3 - r 5 5

Aplicando os limites de integração

∫ 0 2 4 r 2 - r 4 d r = 4 2 3 3 - 2 5 5 - 4 0 3 3 - 0 5 5

∫ 0 2 4 r 2 - r 4 d r = 64 15

Integrando o resultado com relação a θ

∫ 64 15 d θ = 64 θ 15

Aplicando os limites...

∫ 0 2 π 64 15 d θ = 64 2 π 15 - 64 0 15

∫ 0 2 π 64 15 d θ = 128 π 15

Portanto, a massa do solido é dado por 128 π 15 .

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

m = 128 π 15

Exercícios de Livros Relacionados

Expresse o volume da cunha no primeiro octante que é cortada do cilindro y 2 + z 2 = 1 pelos planos y = x e x = 1 como uma integral tripla.Utilize a Tabela de Integrais (nas Páginas de referência 6-10
Use a Regra do Ponto Médio para as integrais triplas (Exercício 24) para estimar o valor da integral. Divida B em oito subcaixas de igual tamanho. ∭ B 1 ln ⁡ ( 1 + x + y + z ) d V onde B = x , y , z |
Na Regra do Ponto Médio para as Integrais Triplas, usamos a soma tripla de Riemann para aproximar a integral tripla em uma caixa B, onde f ( x , y , z ) é calculada no centro ( x - i , y - j , z - k )
A função densidade conjunta das variáveis aleatórias X ,Y e Z é f x , y , z = C x y z se 0 ≤ x ≤ 2 , 0 ≤ y ≤ 2 , 0 ≤ z ≤ 2 e f x , y , z = 0 caso contrário.Determine o valor da constante C .Determine
Use a Regra do Ponto Médio para as integrais triplas (Exercício 24) para estimar o valor da integral. Divida B em oito subcaixas de tamanho igual. ∭ B x e x y z d V Onde B = x , y , z | 0 ≤ x ≤ 4,0 ≤