UFF, Volta Redonda, Cálculo Diferencial e Integral II, Listas Cálculo Diferencial e Integral II - Lista 2 - Integral Tripla - 2019.1, Questão 2.
2- Use integral tripla para calcular o volume do sólido acima do plano , limitado por e pelos planos e .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nessa questão, queremos calcular o volume formado acima do plano e limitado pelos planos , e .
E aí, lembra como calculamos isso? 😊
Para calcular o volume a partir de uma integral tripla, aplicamos
Onde é a região limitada e .
Então o que precisamos fazer é definir os limites de integração em , e e aplicar na integral.
Entendeu? Bora começar! 😁
Passo 2
Primeiro vamos visualizar a região de integração.
Estamos interessados na região limitada por , , e acima do plano . Ou seja
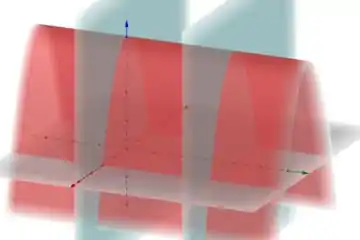
Em , vemos que é limitado entre e e entre e .
Já a altura do solido é dada entre e , ou seja, montando a integral temos
Calculando a primeira integral
Aplicando os limites de integração
Integrando o resultado em relação a ...
Aplicando os limites de integração de
Bacana, não é? 😎
Passo 3
Por fim, integrando o resultado em função de ...
Aplicando os limites de integração
Portanto, o volume do solido do problema é
Fim! Iae, o que achou? Responde Aí! 😁
