UFF, Volta Redonda, Cálculo Diferencial e Integral II, Listas Cálculo Diferencial e Integral II - Lista 2 - Integral Tripla - 2019.1, Questão 5.
5- Calcule o volume do sólido limitado pelos paraboloides e .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema estamos interessados em calcular o solido limitado pelos paraboloides e .
Tem alguma ideia do que podemos fazer? 🤔
A primeira coisa a se fazer, é visualizar o solido que estamos interessados. Depois disso, aplicamos os métodos necessários para obter o volume do solido que é formado.
Já adianto que para esse caso, vamos usar simetrias cilíndricas para calcular a integral volumétrica.
Sacou? Bora lá! 😁
Passo 2
O paraboloide tem seu vértice na origem do sistema e possui concavidade voltada para cima. Já o paraboloide possui seu vértice em e corta o eixo e o eixo em .
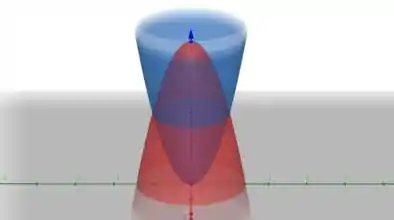
A projeção desse solido no plano resulta em um círculo, daí podemos ver que a simetria cilíndrica vai nos ajudar.
Para converter nosso problema de coordenadas cartesianas para coordenadas cilíndricas, fazemos
Antes de montar a integral, temos que definir os limites de integração para e . Para é mais simples, pois na figura vemos que a projeção do solido varia de a , mas para obter a variação de temos que igualar as duas equações
Ou seja, varia de a .
Lembra do jacobiano que deve ser multiplicado à função de integração quando convertemos as coordenadas!
Passo 3
Integrando com relação a e aplicando os limites de integração
Substituindo o resultado na integral
Convertendo as coordenadas e multiplicando o jacobiano, temos
Integrando com relação a
Aplicando os limites de integração
E por último, temos
Portanto, o volume do solido é !
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
