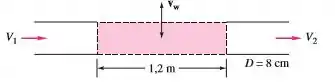
Água escoando por um tubo com de diâmetro entra em uma seção porosa, como mostra a figura abaixo, que permite uma velocidade radial uniforme através das superfícies das paredes por uma distância de . Se a velocidade média na entrada for igual a , determine a velocidade de saída se para fora do tubo ou para dentro do tubo. Qual valor de fará ?

Calcularemos cada vazão separadamente, a começar por que é a mais simples.

Lembramos que a vazão é dada pelo produto da área da seção e da velocidade média do fluido.

Nos é passado que basta então calcular .

Como a área é de um círculo de diâmetro

Logo se :

A vazão possui a mesma área, ou seja,

Então

Agora para a vazão , devemos utilizar outra área para o escoamento.

Como o tubo é cilíndrico devemos calcular a área da superfície de saída/entrada como sendo a casca do cilíndro:

Onde .

O que nos dá uma vazão de:

Na letra a seção porosa trabalha como saída, então:

Sabemos que:

Para :

Logo

Na letra a seção porosa trabalha como entrada, então:

Se :

Para a letra calcularemos dado que :

Como não sabemos se é de entrada ou saída, vou supor que seja de saída:

Repare que nossa suposição estava correta. Caso fosse negativo, seria de entrada.