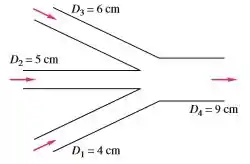
Três tubos fornecem água em regime permanente a para um tubo maior de saída mostrado na figura abaixo. A velocidade e a vazão de saída . Encontre , e se sabemos que aumentando em aumentará em .
Passo 1
Novamente temos um escoamento em um sistema. E como sabemos que a água é um fluido incompressível a , então temos que a vazão de entrada é igual a vazão de saída. Podemos escrever isso como:
Vamos agora isolar o que temos para um lado e o que não temos para o outro. Como o enunciado deu e (com o qual a gente pode descobrir ), temos:
O problema é que a vazão dada de está em e a velocidade do fluido em foi dada em ,assim precisamos passar a vazão para .
E já que estamos aqui, vamos calcular o e matar logo o item c:
Se liga que a gente passou aquele diâmetro que estava em cm pra metro antes de resolver, falou?
Passo 2
Agora vamos usar o fato que “se sabemos que aumentando em aumentará em ”. Olha só o que isso significa... Atualmente temos que:
Se aumentarmos :
E podemos fazer a segunda equação menos a primeira, obtendo:
Então um aumento de da vazão de água em é igual a um aumento de 0,1 da vazão em .
Como sabemos , conseguimos achar .
Agora para achar a velocidade de vazão basta dividir a vazão pela área.
Passo 3
Finalmente podemos resolver o primeiro item:
Como sabemos , e conseguimos saber o valor de , pois lá no inicio montamos a equação de entradas e saídas do sistema.
Agora, isolando a incógnita , temos:
Substituindo e :
Agora, sabendo a vazão em , facilmente conseguimos descobrir a velocidade média do fluido nessa região: