Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Vazão e Volume de Controle

Ver Teoria
Exercício 41235678910

Enunciado

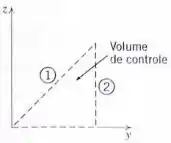
Um campo de velocidade é dado por V → = a z j ^ + b k ^ , onde a = 10   s - 1 e b = 5 m s . Para o volume de controle triangular de 1 m × 1 m   (com profundidade de w = 1   m perpendicular ao diagrama), um elemento de área 1 pode ser representado por w - d z j ^ + d y k ^ e um elemento de área 2 por w d z j ^ .

a   Encontre uma expressão para V → ∙ d A 1 → .

b   Avalie ∫ A 1 V → ∙ d A → 1 .

c   Encontre uma expressão para V → ∙ d A → 2 .

d   Avalie ∫ A 2 V → ∙ d A → 2 .

Passo 1

Calma galera, essa questão é bem mais simples do que parece.

Vou reescrever o que o enunciado falou, colocando na forma de trios ordenados:

V → = a z j ^ + b k ^ = 0 , a z , b

d A 1 → = w - d z j ^ + d y k ^ = 0 , - w d z , w d y

d A → 2 = w d z j ^ = ( 0 , w d z , 0 )

Substituindo os valores de a ,   b e w e tirando a coordenada x dos vetores (todas são nulas)

V → = ( 10 z , 5 )

d A 1 → = - d z , d y

d A → 2 = ( d z , 0 )

Passo 2

Na letra a é pedido para calcularmos V → . d A 1 → :

Fazendo o produto escalar:

V → ∙ d A 1 → = ( 10 z , 5 ) ∙ - d z , d y

V → ∙ d A 1 → = - 10 z d z + 5 d y

Na letra b é pedido para calcularmos aquela integral:

∫ A 1 V → ∙ d A → 1 = ∫ A 1 - 10 z d z + 5 d y

Sabemos que 0 < z < 1 e que 0 < y < 1 , logo:

∫ A 1 V → ∙ d A → 1 = ∫ 0 1 - 10 z d z + ∫ 0 1 5 d y

∫ A 1 V → ∙ d A → 1 = - 10 z ² 2 0 1 + ( 5 y ) 0 1

∫ A 1 V → ∙ d A → 1 = - 5 + 5 = 0

Passo 3

Calculamos outro produto escalar, agora o da letra c :

V → ∙ d A → 2 = 10 z , 5 ∙ d z , 0

V → ∙ d A → 2 = 10 z d z

Logo a expressão pedida em d :

∫ A 2 V → ∙ d A → 2 = ∫ 0 1 10 z   d z

∫ A 2 V → ∙ d A → 2 = 10 z ² 2 0 1

∫ A 2 V → ∙ d A → 2 = 5

Resposta

a   V → ∙ d A 1 → = - 10 z d z + 5 d y

b   ∫ A 1 V → ∙ d A → 1 = 0

c   V → ∙ d A → 2 = 10 z d z

d   ∫ A 2 V → ∙ d A → 2 = 5

Exercícios de Livros Relacionados

Uma chapa fina deve passar de forma contínua num banho de tinta contido num reservatório, como mostra a figura. Em regime permanente, o diagrama de velocidades bidimensional v z = f x é tal que, numa
No escoamento turbulento de um fluido em condutos circulares, o diagrama de velocidades é dado pela equação v = v m á x 1 - r R 1 / 7 á , onde todas as grandezas têm o mesmo significado do Exercício 3
O ar escoa num tubo convergente. A área da maior seção do tubo é 20c m 2 e a 3 da menor é 10c m 2 . A massa específica do ar na seção 1 é 1,2k g / m 3 , enquanto na seção 2 é 0,9k g / m 3 . Sendo a ve
Um tubo admite água ( ρ = 1000k g / m 3 ) num reservatório com uma vazão de 20L / s . No mesmo reservatório é trazido óleo ( ρ = 800k g / m 3 ) por outro tubo com uma vazão de 10L / s . A mistura homo
Um propulsor a jato queima 1k g / s de combustível quando o avião voa à velocidade de 200m / s . Sendo dados ρ a r = 1,2k g / m 3 , ρ g = 0,5k g / m 3 (na seção 2 ), A 1 = 0,3m 2 e A 2 = 0,2m 2 , dete