Exercícios Resolvidos de Vazão e Volume de Controle

Exercício 7 1 2 3 4 5 6 8 9 10

Enunciado

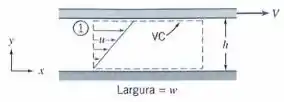
(a) Obtenha expressões para a vazão volumétrica para o fluxo de quantidade de movimento através da secção transversal do volume de controle mostrado no diagrama.

Para o escoamento do item anterior, obtenha uma expressão para o fluxo de energia cinética, , através da seção transversal do volume de controle mostrado.

Passo 1

Para calcularmos a vazão volumétrica devemos utiliza a expressão:

Pela figura temos que o elemento de área é:

E é definido apenas por sua componente horizontal .

Passo 2

Podemos dizer pela figura que

Com as seguintes condições de contorno:

Subsituindo na expressão de :

Logo,

Passo 3

Substituindo na expressão da vazão:

Passo 4

Na letra é pedido para que calculemos o fluxo de energía cinética dado pela fómula:

Subsituindo nossas expressões de e :

Arrumando a casa:

Resposta

Exercícios de Livros Relacionados

Uma chapa fina deve passar de forma contínua num banho de tinta contido num reservatório, como mostra a figura. Em regime permanente, o diagrama de velocidades bidimensional v z = f x é tal que, numa

No escoamento turbulento de um fluido em condutos circulares, o diagrama de velocidades é dado pela equação v = v m á x 1 - r R 1 / 7 á , onde todas as grandezas têm o mesmo significado do Exercício 3

O ar escoa num tubo convergente. A área da maior seção do tubo é 20c m 2 e a 3 da menor é 10c m 2 . A massa específica do ar na seção 1 é 1,2k g / m 3 , enquanto na seção 2 é 0,9k g / m 3 . Sendo a ve

Um tubo admite água ( ρ = 1000k g / m 3 ) num reservatório com uma vazão de 20L / s . No mesmo reservatório é trazido óleo ( ρ = 800k g / m 3 ) por outro tubo com uma vazão de 10L / s . A mistura homo

Um propulsor a jato queima 1k g / s de combustível quando o avião voa à velocidade de 200m / s . Sendo dados ρ a r = 1,2k g / m 3 , ρ g = 0,5k g / m 3 (na seção 2 ), A 1 = 0,3m 2 e A 2 = 0,2m 2 , dete