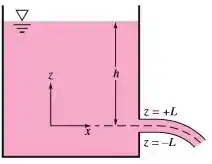
Quando um jato líquido, regido pela gravidade, sai de uma fenda em um tanque, como na figura abaixo, uma aproximação para a distribuição de velocidade na saída é
onde é a profundidade da linha de centro do jato. Próximo à fenda, o jato é horizontal, bidimensional, e de espessura , como mostrado. Encontre uma expressão geral para a vazão volumétrica total que sai da fenda.
Passo 1
Nesta questão devemos aplicar a expressão que define a vazão que passa por uma área:
No caso a velocidade é e como o jato é bidimensional vamos dizer que
Sendo que é uma largura que “sai” da tela.
Passo 2
Em seguida devemos resolver nossa integral substituindo as informações que temos:
Se ,
Podemos tirar e de dentro da integral:
Vamos realizar a substituição e . (Obs.: nossos limites de integração também vão mudar...Como varia de até , irá variar de até )