Em um sistema de movimentação de ar apresentado na figura há entrada de ar pela seção 1-1, seguida de um trocador de calor que pode aquecer o ar (condição A) ou não aquecer (condição B). Em seguida o ar é inserido em uma caixa de distribuição de ar podendo escoar para três saídas nas seções 3-3, 4-4 e 6-6. Na seção 5-5 há um pistão que pode movimentar-se ou estar travado em repouso. Na seção 6-6 há um tubo de Pitot posicionado de modo a medir uma velocidade que tem um valor muito próximo ao valor da velocidade média nesta seção transversal, seguido por um ventilador auxiliar.
São dados:
- Na seção 1-1: Vazão em massa , massa específica e área
- Na condição A o trocador de calor aquece o ar e sua massa específica na seção 2-2 é
- As áreas das seções de saída são: e
Pede-se:
- Para condição B em que o ar não é aquecido e o pistão está travado, e considerando que as vazões em massa de saída são neste caso, determinar qual a vazão volumétrica Q6 e a velocidade média V6
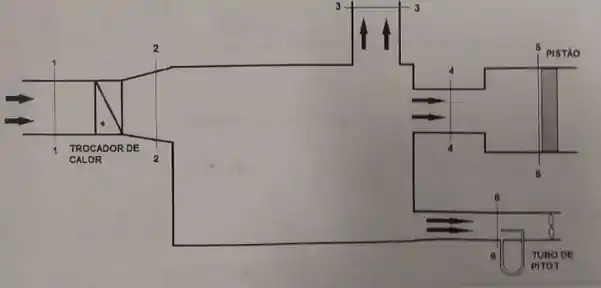
Passo 1
Sem aquecimento, o que a gente já consegue identificar de cara?
Que a densidade de entrada vai ser igual a densidade na seção 2, certo?
Sem movimento do pistão, é como se a seção 4-4 estivesse tapa, então na prática, o balanço de massa vai nos dar que:
Passo 2
O enunciado nos diz que
Substituindo no balanço de massa teremos:
Sabe-se pelo enunciado que a vazão mássica 1 vale 6 kg/s e portanto,
Consequentemente, podemos substituir agora na equação da vazão mássica no ponto 6 e assim, temos:
Dada a relação entre vazão mássica, volumétrica e velocidade por:
Note que o valor da densidade na saída 6 deve ser igual ao valor da entrada 1, uma vez que não há aquecimento.