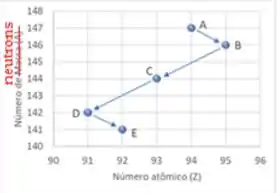
3. O gráfico ao lado mostra o decaimento em série do radionuclídeo para o radionuclídeo .
a. Escreva a equação completa para o decaimento envolvido em cada uma das 4 etapas.
b. Sabendo que o nuclídeo possui massa atômica igual a e que o nuclídeo possui massa atômica igual a , calcule a energia liberada no processo para .
Passo 1
- Oi, galerinha! Tudo bom? Vamos entender o gráfico! Note que no eixo temos o número atômico do átomo e no eixo temos o número de nêutrons . Deste modo, podemos saber a massa do átomo fazendo:
- Aqui temos que calcular a energia liberada de para . Para isso temos que calcular primeiro a diferença de massa:
Sendo assim, podemos calcular a massa e o número atômico de cada espécie, fica assim:
Agora que já sabemos as massas e números atômicos podemos descobrir quem são as partículas fazendo a diferença do antes e depois.
Passo 2
Começando pela primeira etapa, vamos escrever a seguinte equação genérica:
Aqui temos formando e liberando uma partícula . Pelo balanço de massa, temos que a massa da partícula tem que ser . Já o número prótons aumenta em uma unidade, então pelo balanço temos que a partícula tem . Logo temos a seguinte reação:
Agora podemos aplicar o mesmo raciocinio para as outras etapas:
Vamos para letra b!
Passo 3
Considerando que a massa da partícula é de
Agora podemos calcular a energia por:
O sinal negativo indica que a energia foi liberada, ok!
Resposta
a.
b.