Uma esfera homogênea feita de poeira (podemos penetrá-la) tem massa e raio . Sendo a constante gravitacional de Newton, qual é o módulo da aceleração que uma partícula pontual localizada a uma distância do centro da esfera sentirá por conta da atração gravitacional da esfera?
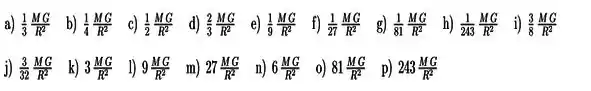
Passo 1
Vimos que o que contribui para a força que a partícula vai experimentar é a massa interna. Sendo assim, temos que calcular qual é a massa que está dentro da esfera de raio .
Para isso vamos calcular a densidade volumétrica da esfera de poeira.
Agora que temos a densidade volumétrica, temos que multiplicar pelo volume o qual queremos a massa interna. Para assim obter a massa interna.
Assim a força experimentada por esse ponto é
Lembrando que pela segunda lei de Newton
Então a aceleração é
Agora só falta substituir o valor da massa interna, que vimos que é
Resposta
Alternativa