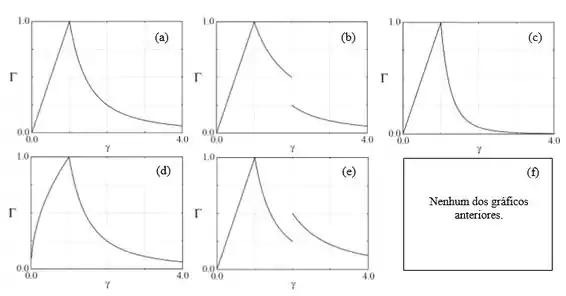
Uma partícula de massa encontra-se a uma distância do centro de uma distribuição esferossimétrica de massa. Essa distribuição consiste de uma massa uniforme sobre uma casca esférica de raio , concêntrica com outra massa uniforme em uma esfera maciça de raio . Seja o módulo da força gravitacional sobre . Que gráfico representa a razão , como função de ?
Passo 1
Primeiro vamos desenhar para entender o que está acontecendo.
Existem três possibilidades:
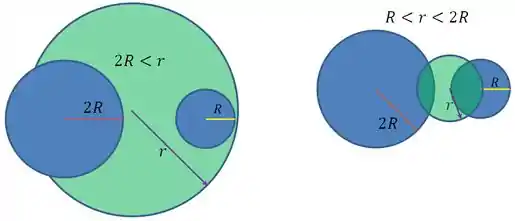
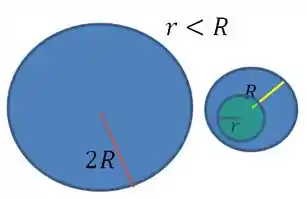
Agora com o auxilio do desenho vai ficar mais tranquilo analisarmos a questão. A força é dada pela fórmula:
No primeiro caso a massa dentro da esfera de raio é a massa das duas esferas , assim:
No segundo caso a massa dentro da esfera de raio é apenas a massa da esfera de raio , assim a massa interna a esfera é apenas .
Esse é o caso problemático, pois a massa interna a esfera de raio terá de ser calculada pela densidade volumétrica.
Se tivéssemos um fio de volume e massa e quiséssemos saber a densidade faríamos , certo? Assim conseguiríamos descobrir a massa correspondente para qualquer volume daquele material, bastando fazer:
Faremos o mesmos para esse caso, lembrando que o volume de uma esfera é .
Assim a densidade volumétrica da esfera de raio será de
Como queremos saber a massa dentro da esfera de raio , iremos multiplicar essa densidade pelo volume da esfera de raio . Assim,
Agora que encontramos a massa interna a esfera de raio , podemos calcular a força:
Passo 2
Ainda não terminamos a questão porque o professor fez uma graça em colocar o eixo do gráfico sendo , onde .
Assim, temos que calcular e deixa-lo em função de que é o eixo do gráfico e vale .
No primeiro caso temos:
No segundo caso temos:
No terceiro caso temos:
Passo 3
Agora temos que montar o gráfico, e para isso temos que analisar a função que terminamos de encontrar para cada trecho.
O primeiro trecho é o que tem menor , ou seja, o terceiro caso onde o raio está entre e .
A função nesse trecho é
Essa é a função de uma reta, é igual a . Então nosso gráfico será uma reta entre
Pois o que varia é o assim, temos que
Já eliminamos a opção . Já que seu primeiro trecho não é uma reta.
Vamos continuar, o segundo trecho será descrito pela função do segundo caso, pois o está entre . Assim, o está entre:
Nesse trecho a função é:
É uma hipérbole decrescente, que sai do e vai até .
Assim, eliminamos os gráficos , pois eles não têm valor quando.
Por último, vamos analisar o último trecho, onde .
A função desse trecho é:
Que é uma hipérbole decrescente, que sai do 0,5 e vai até 0,125.
Assim, o único gráfico correto é o
Resposta
Alternativa