A figura ao lado ilustra uma sistema composto por 2 massas. A localizada na origem é uma massa pontual de massa M, a outra é uma casca esférica espessa centrada na origem, onde a é seu raio interno e b o raio externo. A casca possui densidade de massa uniforme . Uma partícula de prova de massa m é colocada em 2 regiões distintas no espaço, e . Assinale abaixo a alternativa que contém o módulo da força gravitacional resultante correta sobre a partícula de prova nas regiões e respectivamente.
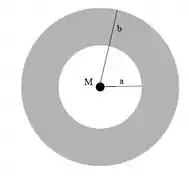
a) e
b) e
c) e
d) e
e) 0 e
f) 0 e
Passo 1
Primeiro vamos pensar no interior da casca esférica.
Nessa região, a massa de prova só vai ser atraída pela massa pontual. Então:
Lembrando que dentro da casca esférica a força gravitacional devida à casca esférica é zero, por causa da simetria da esfera (as forças atrativas se anulam).
E no exterior da esfera?
Aí vamos ter força gravitacional devida à massa pontual e à casca. A força devido à massa pontual vai ser igual à que já calculamos:
A força devida à casca vai ser:
E a massa da casca vai ser:
Substituindo:
A força total então vai ser:
Ou seja, as forças serão: e
Resposta
Letra A.